Data visualization in Python (pyplot)

Looking ahead: Weeks 3-4

• In week 3, we’ll dive deep into data visualization.

  • How do we make visualizations in Python?

  • What principles should we keep in mind?

• In week 4, we’ll work on managing and cleaning our data.

  • How do I deal with missing values?

  • What are some basic ways to describe my data?

I view both these weeks as integral to Exploratory Data Analysis in Python.

Goals of this lecture

• What is data visualization and why is it important?

• Introducing matplotlib.

• Univariate plot types:

  • Histograms (univariate).

  • Scatterplots (bivariate).

  • Bar plots (bivariate).

Introduction: data visualization

What is data visualization?

Data visualization refers to the process (and result) of representing data graphically.

For our purposes today, we’ll be talking mostly about common methods of plotting data, including:

• Histograms

• Scatterplots

• Line plots

• Bar plots

Why is data visualization important?

• Exploratory data analysis

• Communicating insights

• Impacting the world

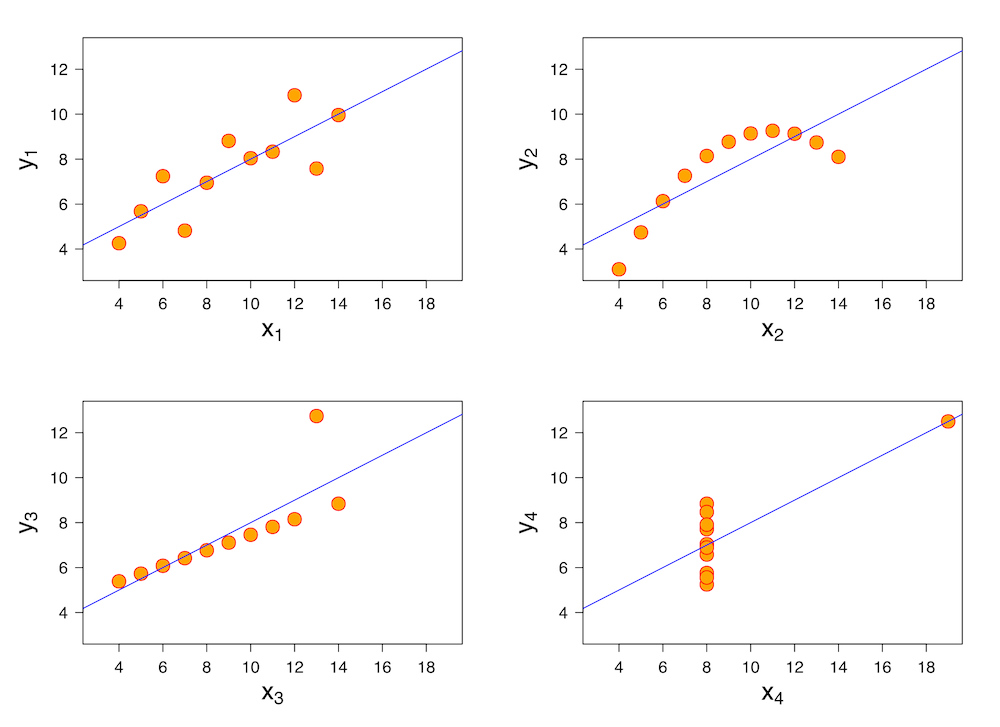
Exploratory Data Analysis: Checking your assumptions

Anscombe’s Quartet

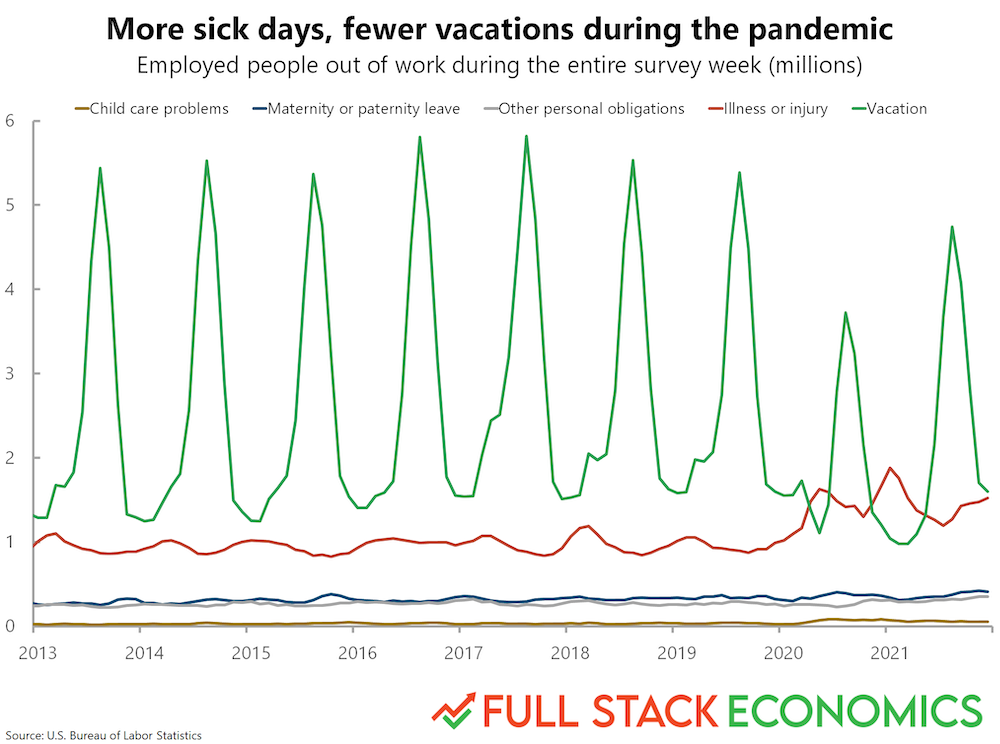
Communicating Insights

Reference: Full Stack Economics

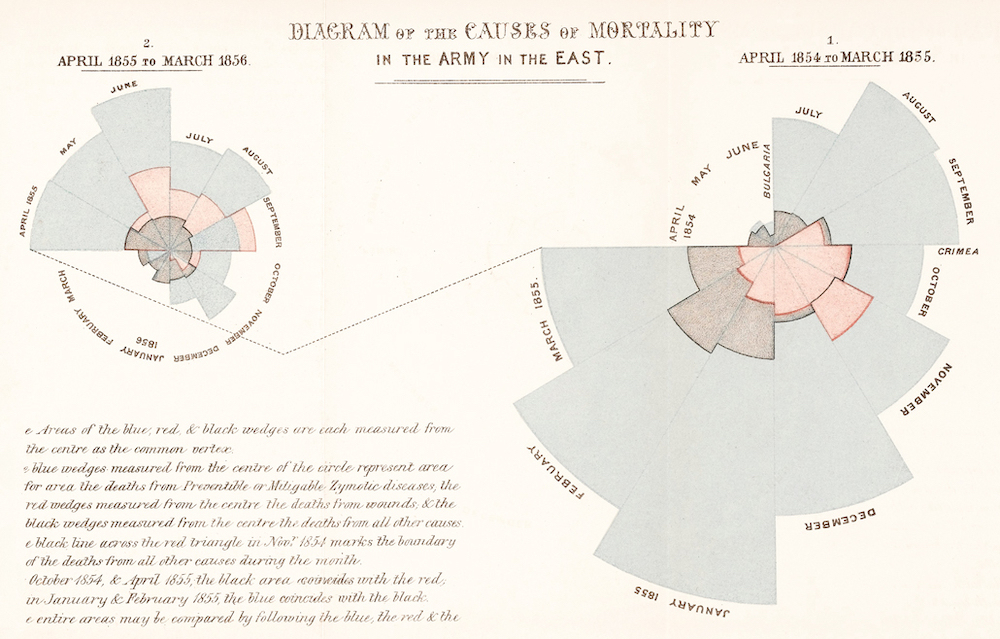
Impacting the world

Florence Nightingale (1820-1910) was a social reformer, statistician, and founder of modern nursing.

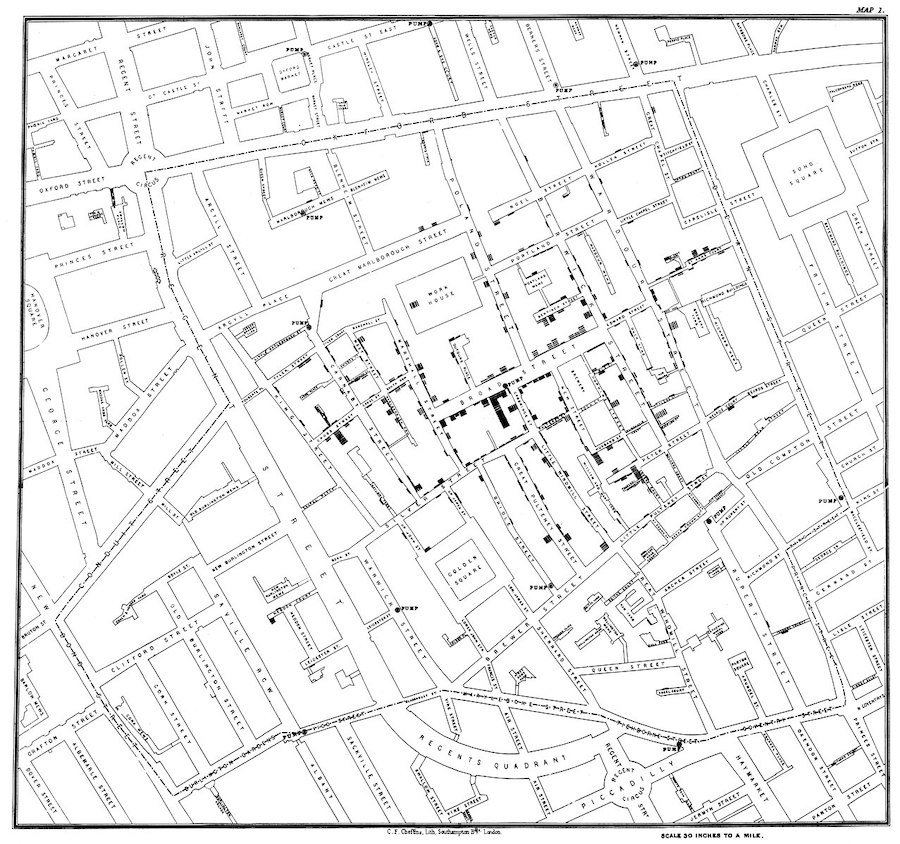
Impacting the world (pt. 2)

John Snow (1813-1858) was a physician whose visualization of cholera outbreaks helped identify the source and spreading mechanism (water supply).

Introducing matplotlib

Loading packages

Here, we load the core packages we’ll be using.

We also add some lines of code that make sure our visualizations will plot “inline” with our code, and that they’ll have nice, crisp quality.

import numpy as np 
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as ss

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

What is matplotlib?

matplotlib is a plotting library for Python.

• Many tutorials available online.

• Also many examples of matplotlib in use.

Note that seaborn (which we’ll cover soon) uses matplotlib “under the hood”.

What is pyplot?

pyplot is a collection of functions within matplotlib that make it really easy to plot data.

With pyplot, we can easily plot things like:

• Histograms (plt.hist)

• Scatterplots (plt.scatter)

• Line plots (plt.plot)

• Bar plots (plt.bar)

Example dataset

Let’s load our familiar Pokemon dataset, which can be found in data/pokemon.csv.

df_pokemon = pd.read_csv("data/pokemon.csv")
df_pokemon.head(3)

	#	Name	Type 1	Type 2	Total	HP	Attack	Defense	Sp. Atk	Sp. Def	Speed	Generation	Legendary
0	1	Bulbasaur	Grass	Poison	318	45	49	49	65	65	45	1	False
1	2	Ivysaur	Grass	Poison	405	60	62	63	80	80	60	1	False
2	3	Venusaur	Grass	Poison	525	80	82	83	100	100	80	1	False

Histograms

What are histograms?

A histogram is a visualization of a single continuous, quantitative variable (e.g., income or temperature).

• Histograms are useful for looking at how a variable distributes.

• Can be used to determine whether a distribution is normal, skewed, or bimodal.

A histogram is a univariate plot, i.e., it displays only a single variable.

Histograms in matplotlib

To create a histogram, call plt.hist with a single column of a DataFrame (or a numpy.ndarray).

Check-in: What is this graph telling us?

p = plt.hist(df_pokemon['Attack'])

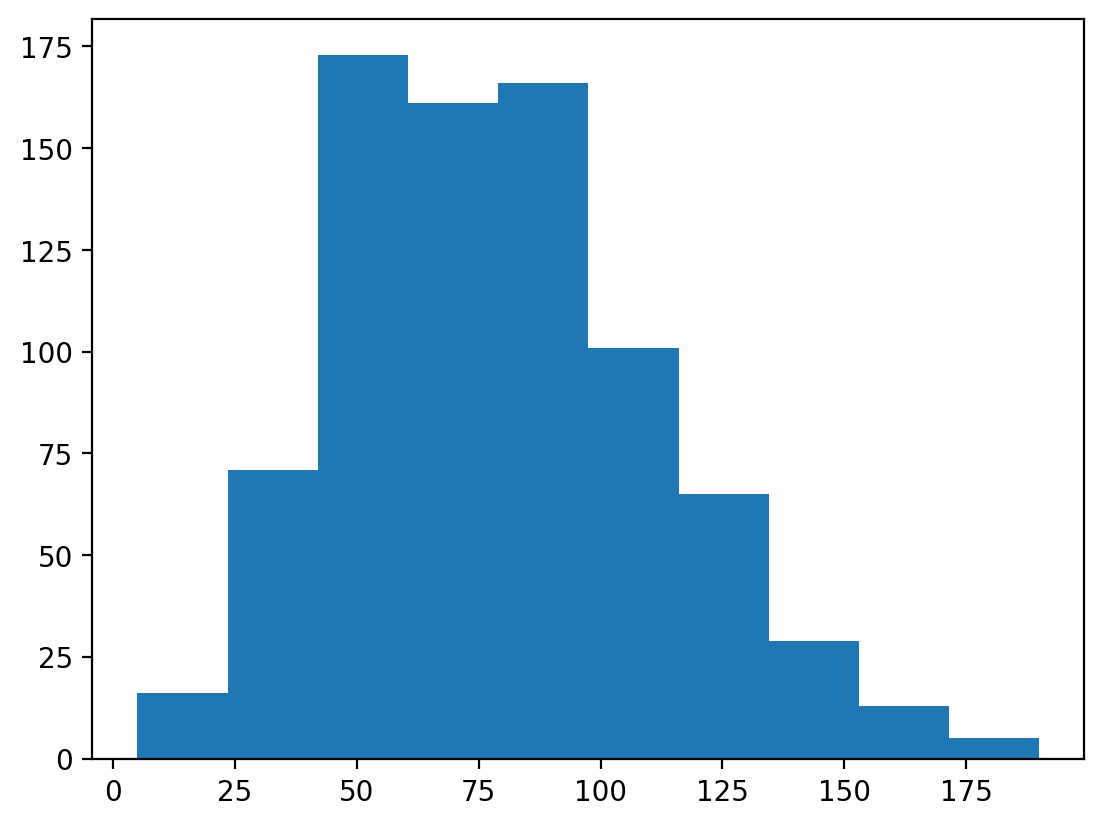
Changing the number of bins

A histogram puts your continuous data into bins (e.g., 1-10, 11-20, etc.).

• The height of each bin reflects the number of observations within that interval.

• Increasing or decreasing the number of bins gives you more or less granularity in your distribution.

### This has lots of bins
p = plt.hist(df_pokemon['Attack'], bins = 30)

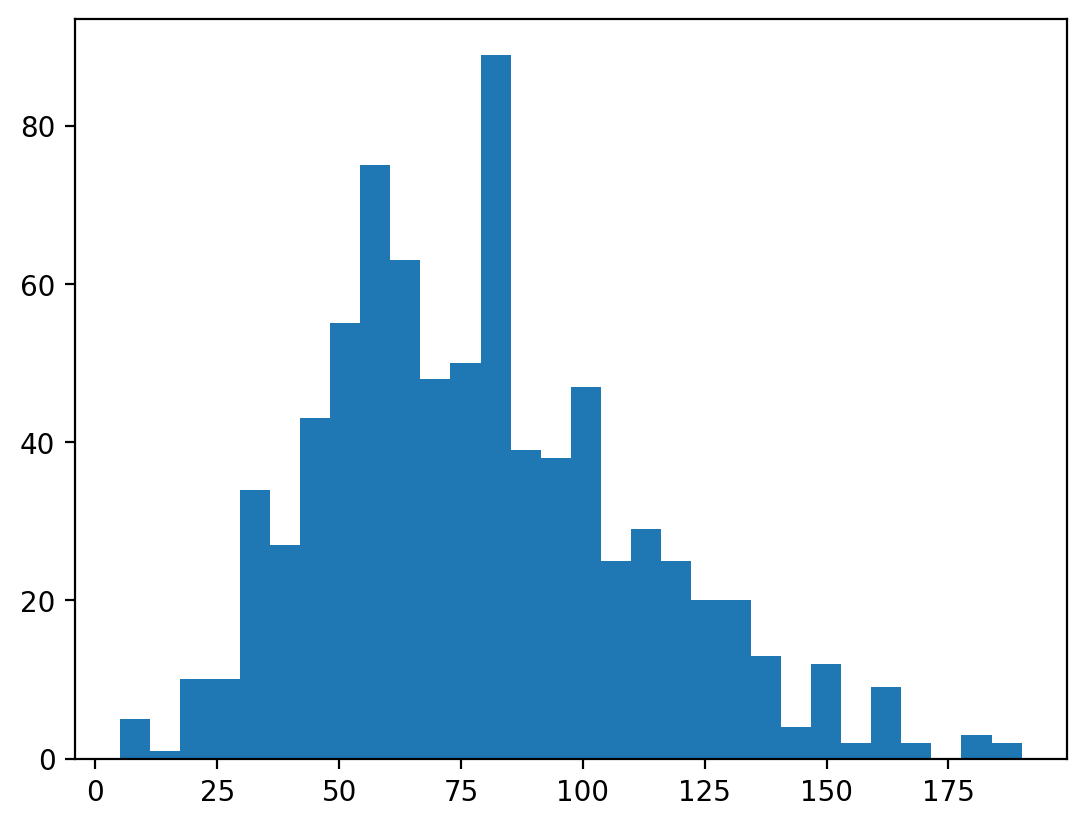
### This has fewer bins
p = plt.hist(df_pokemon['Attack'], bins = 5)

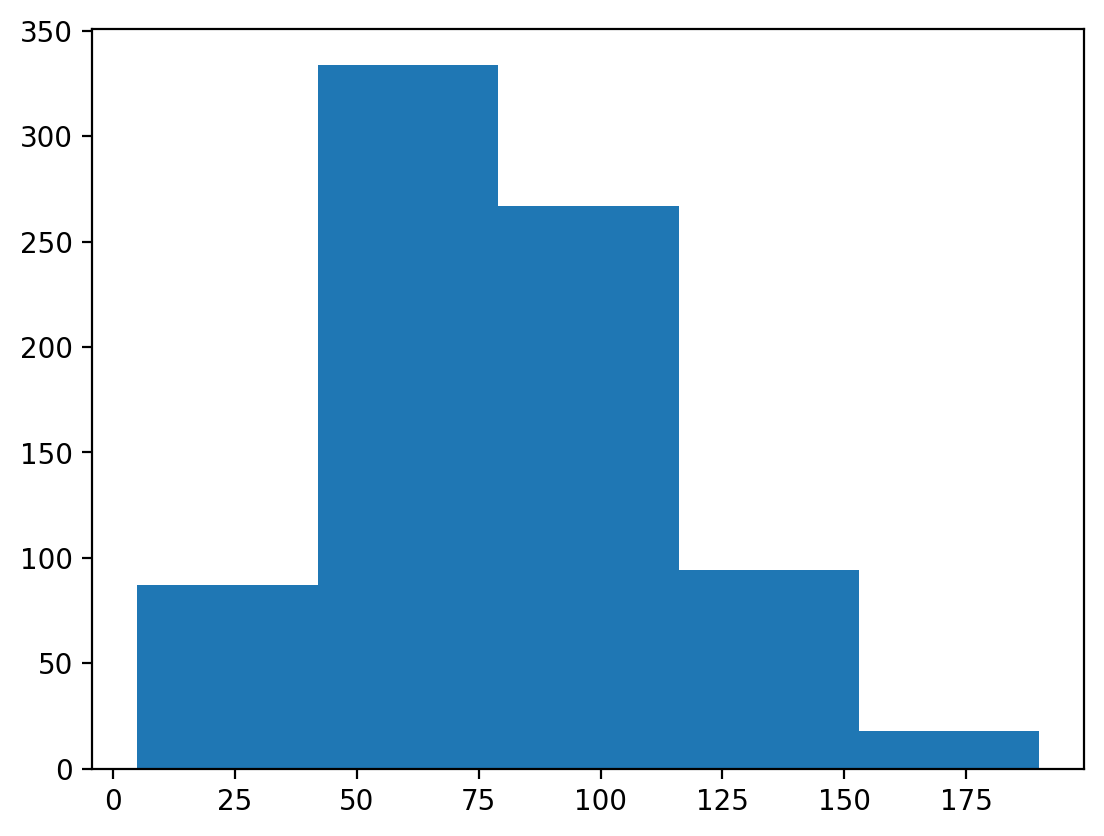
Changing the alpha level

The alpha level changes the transparency of your figure.

### This has fewer bins
p = plt.hist(df_pokemon['Attack'], alpha = .6)

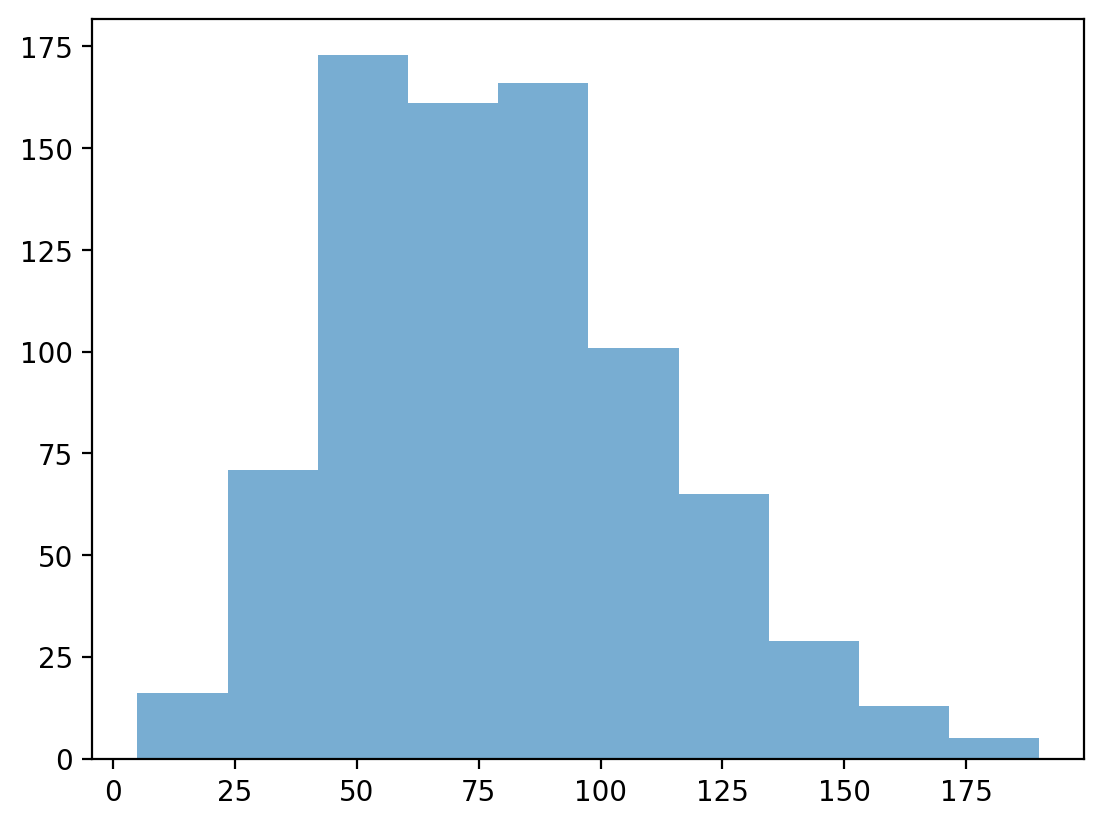
Check-in:

How would you make a histogram of the scores for Defense?

### Your code here

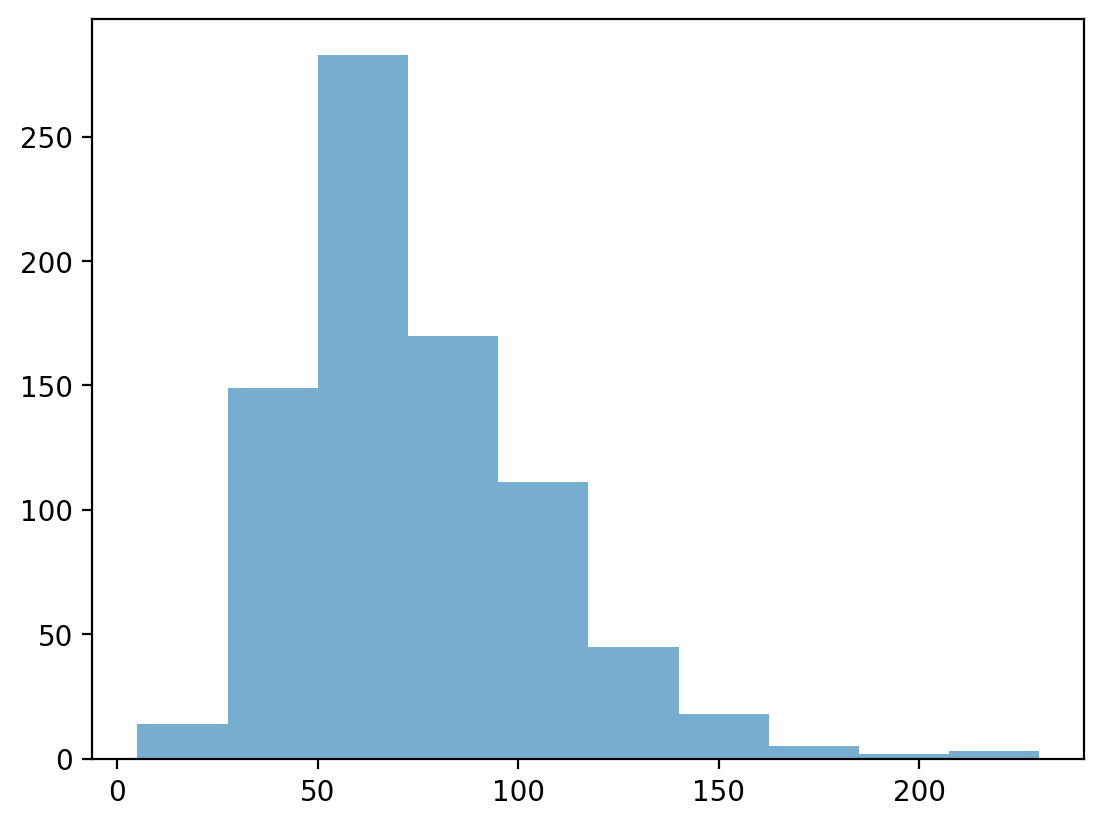
Solution

p = plt.hist(df_pokemon['Defense'], alpha = .6)

Check-in:

Could you make a histogram of the scores for Type 1?

### Your code here

Solution

• Not exactly.

• Type 1 is a categorical variable, so there’s no intrinsic ordering.

• The closest we could do is count the number of each Type 1 and then plot those counts.

Learning from histograms

Histograms are incredibly useful for learning about the shape of our distribution. We can ask questions like:

• Is this distribution relatively normal?

• Is the distribution skewed?

• Are there outliers?

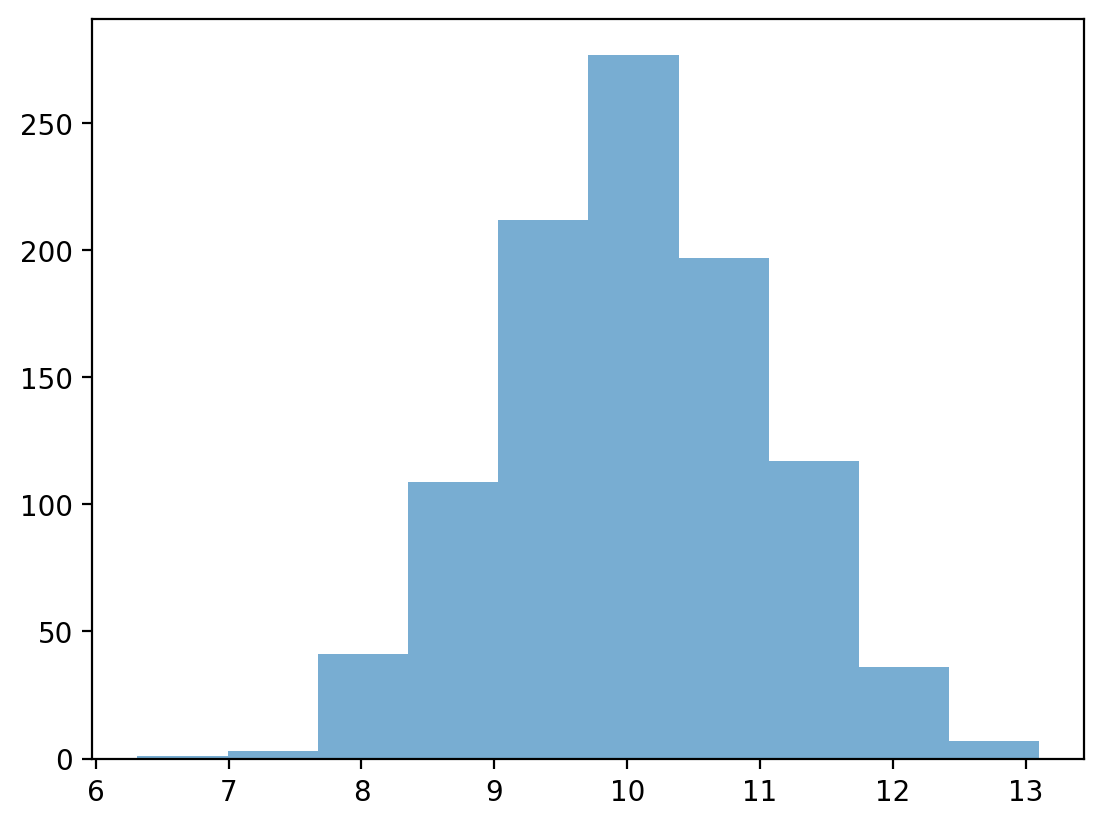
Normally distributed data

We can use the numpy.random.normal function to create a normal distribution, then plot it.

A normal distribution has the following characteristics:

• Classic “bell” shape (symmetric).

• Mean, median, and mode are all identical.

norm = np.random.normal(loc = 10, scale = 1, size = 1000)
p = plt.hist(norm, alpha = .6)

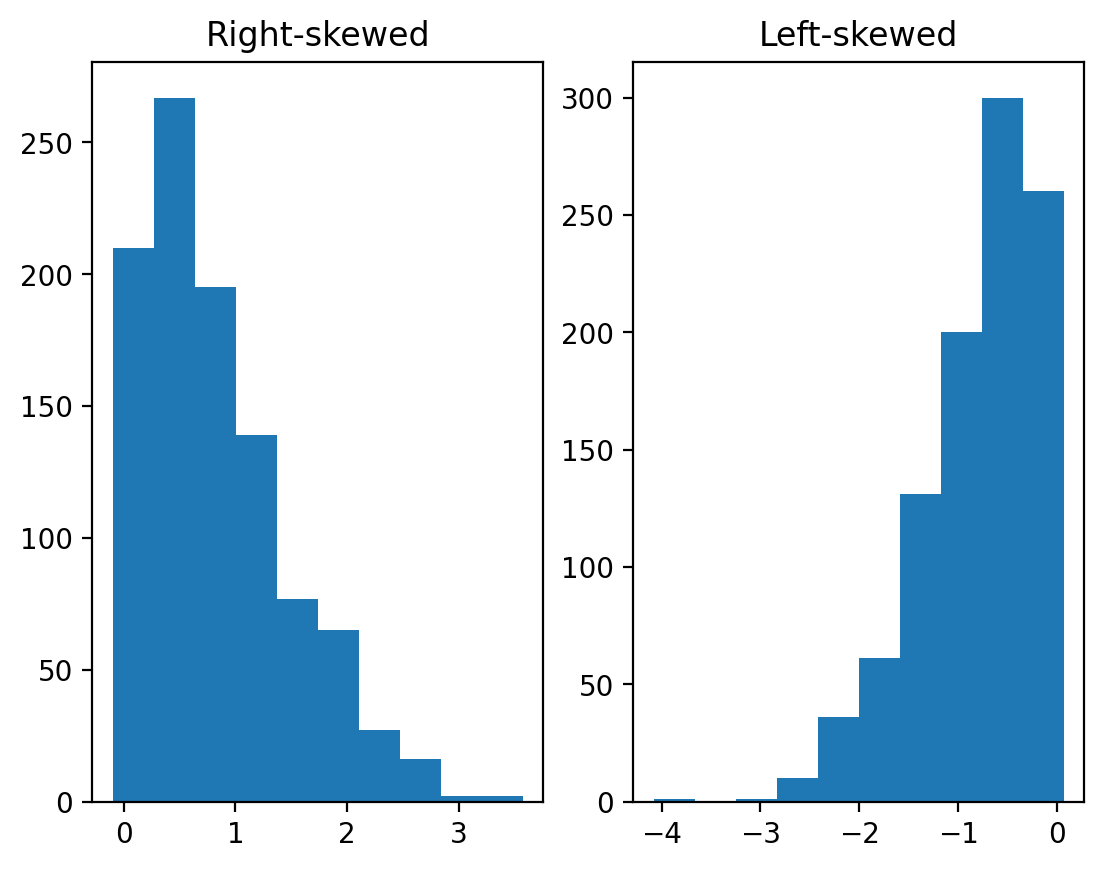
Skewed data

Skew means there are values elongating one of the “tails” of a distribution.

• Positive/right skew: the tail is pointing to the right.

• Negative/left skew: the tail is pointing to the left.

rskew = ss.skewnorm.rvs(20, size = 1000) # make right-skewed data
lskew = ss.skewnorm.rvs(-20, size = 1000) # make left-skewed data
fig, axes = plt.subplots(1, 2)
axes[0].hist(rskew)
axes[0].set_title("Right-skewed")
axes[1].hist(lskew)
axes[1].set_title("Left-skewed")

Text(0.5, 1.0, 'Left-skewed')

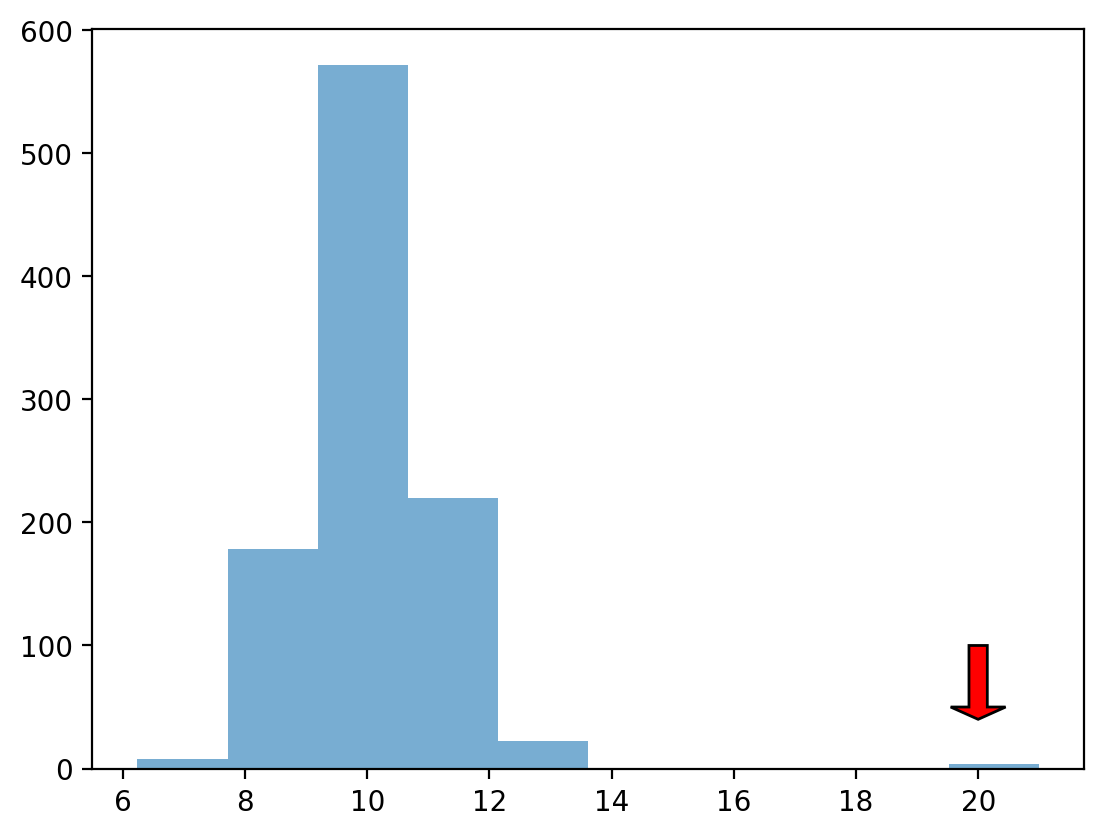
Outliers

Outliers are data points that differ significantly from other points in a distribution.

• Unlike skewed data, outliers are generally discontinuous with the rest of the distribution.

• Next week, we’ll talk about more ways to identify outliers; for now, we can rely on histograms.

norm = np.random.normal(loc = 10, scale = 1, size = 1000)
upper_outliers = np.array([21, 21, 21, 21]) ## some random outliers
data = np.concatenate((norm, upper_outliers))
p = plt.hist(data, alpha = .6)
plt.arrow(20, 100, dx = 0, dy = -50, width = .3, head_length = 10, facecolor = "red")

<matplotlib.patches.FancyArrow at 0x171cee250>

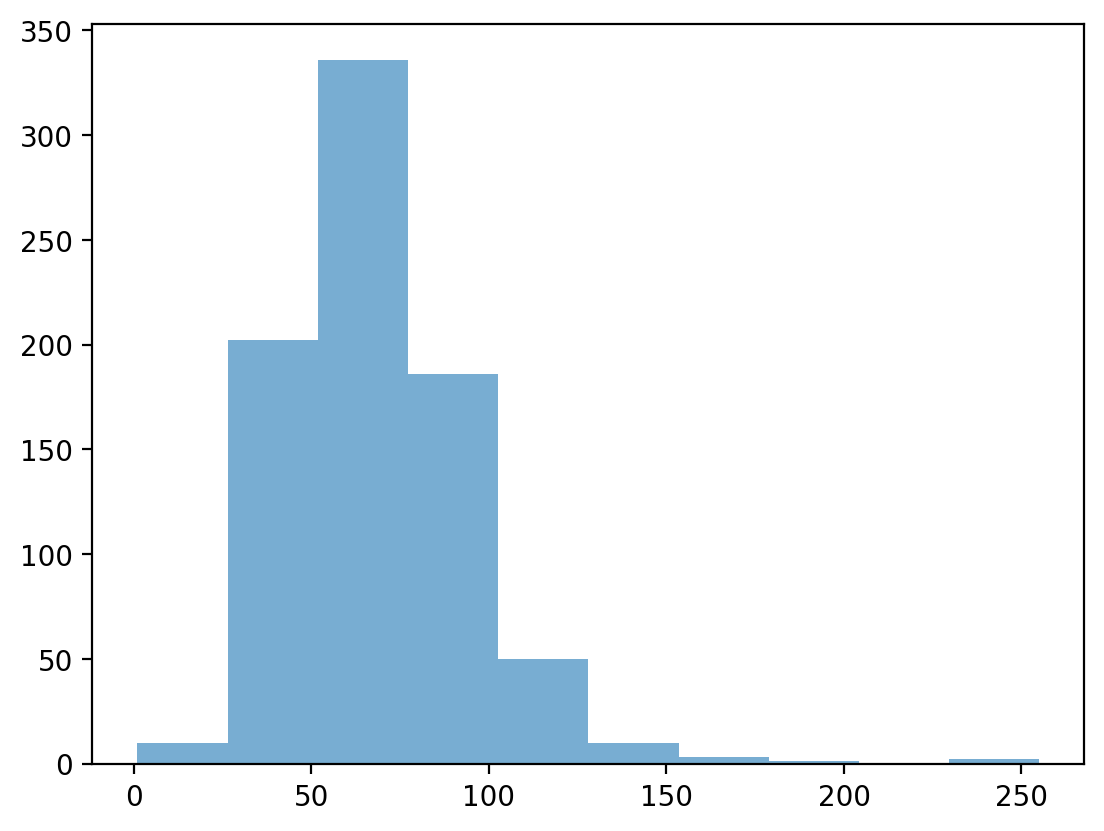
Check-in

How would you describe the following distribution?

• Normal vs. skewed?

• With or without outliers?

p = plt.hist(df_pokemon['HP'], alpha = .6)

Check-in

How would you describe the following distribution?

• Normal vs. skewed?

• With or without outliers?

p = plt.hist(df_pokemon['Sp. Atk'], alpha = .6)

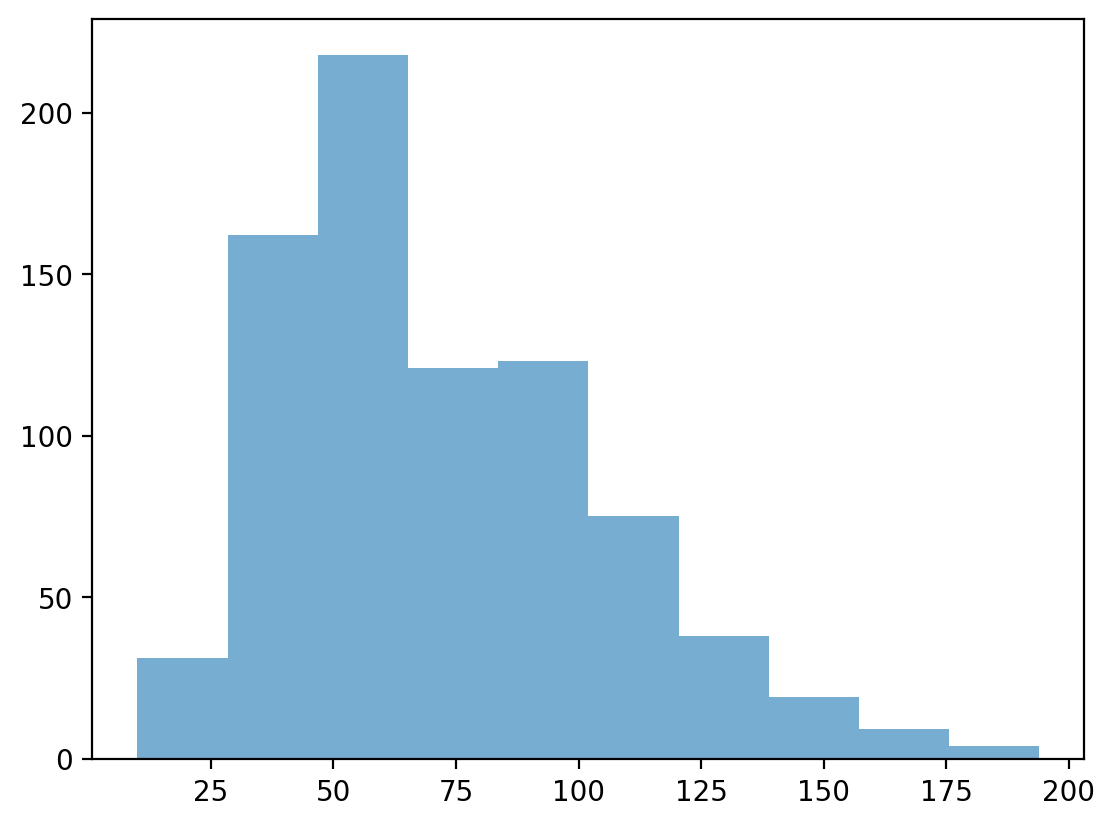
Check-in

In a somewhat right-skewed distribution (like below), what’s larger––the mean or the median?

p = plt.hist(df_pokemon['Sp. Atk'], alpha = .6)

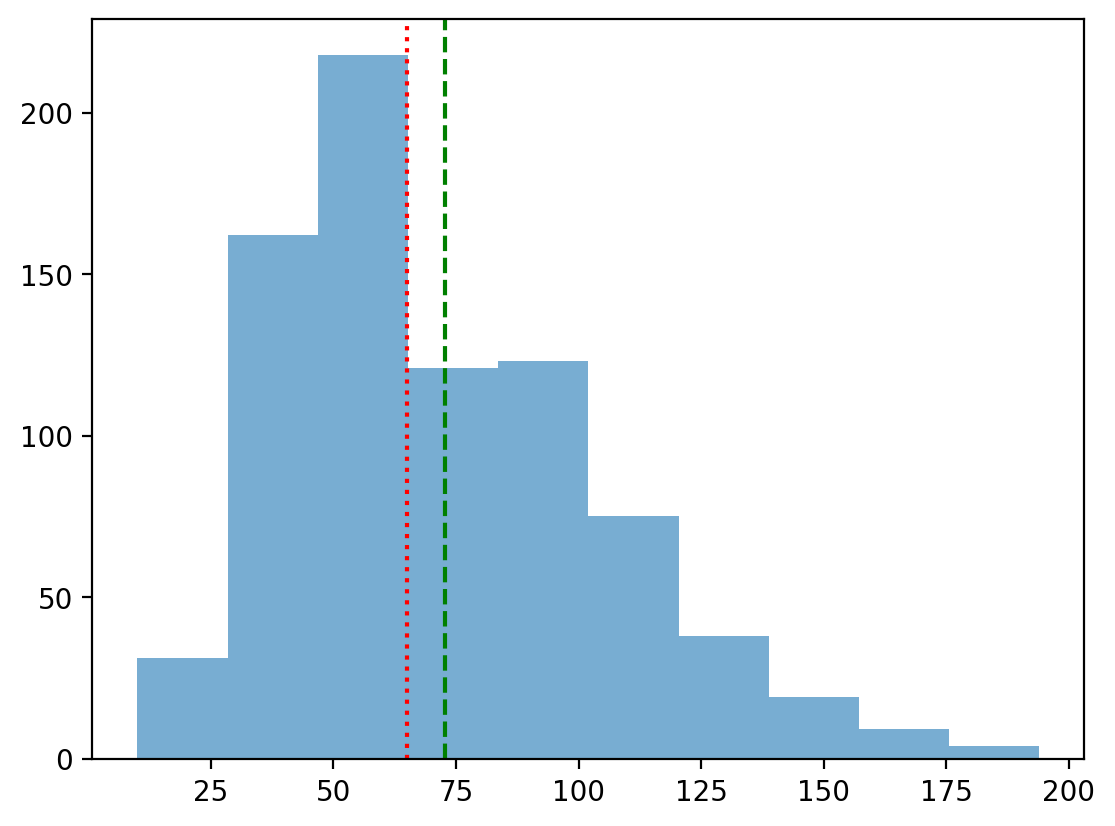
Solution

The mean is the most affected by skew, so it is pulled the furthest to the right in a right-skewed distribution.

p = plt.hist(df_pokemon['Sp. Atk'], alpha = .6)
plt.axvline(df_pokemon['Sp. Atk'].mean(), linestyle = "dashed", color = "green")
plt.axvline(df_pokemon['Sp. Atk'].median(), linestyle = "dotted", color = "red")

<matplotlib.lines.Line2D at 0x1721b7310>

Modifying our plot

• A good data visualization should also make it clear what’s being plotted.

  • Clearly labeled x and y axes, title.

• Sometimes, we may also want to add overlays.

  • E.g., a dashed vertical line representing the mean.

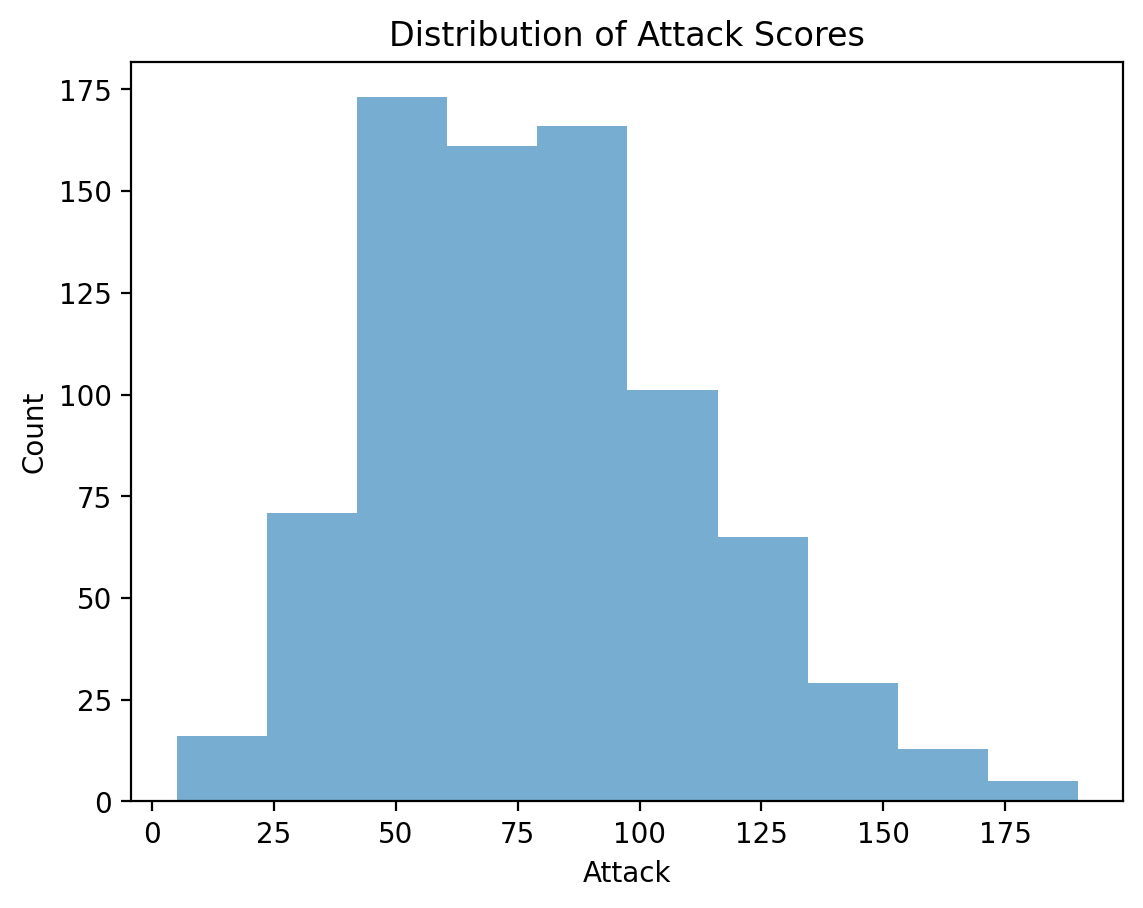
Adding axis labels

p = plt.hist(df_pokemon['Attack'], alpha = .6)
plt.xlabel("Attack")
plt.ylabel("Count")
plt.title("Distribution of Attack Scores")

Text(0.5, 1.0, 'Distribution of Attack Scores')

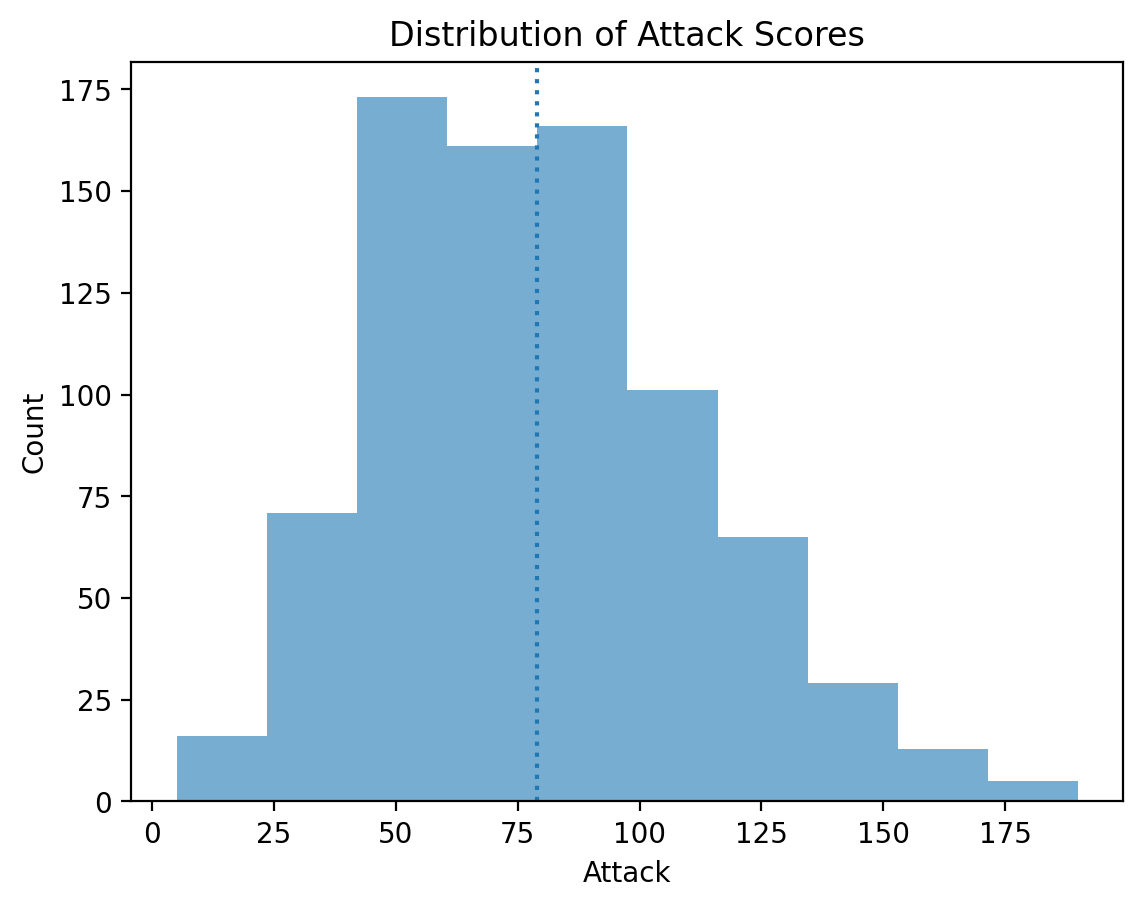
Adding a vertical line

The plt.axvline function allows us to draw a vertical line at a particular position, e.g., the mean of the Attack column.

p = plt.hist(df_pokemon['Attack'], alpha = .6)
plt.xlabel("Attack")
plt.ylabel("Count")
plt.title("Distribution of Attack Scores")
plt.axvline(df_pokemon['Attack'].mean(), linestyle = "dotted")

<matplotlib.lines.Line2D at 0x17255d3d0>

Scatterplots

What are scatterplots?

A scatterplot is a visualization of how two different continuous distributions relate to each other.

• Each individual point represents an observation.

• Very useful for exploratory data analysis.

  • Are these variables positively or negatively correlated?

A scatterplot is a bivariate plot, i.e., it displays at least two variables.

Scatterplots with matplotlib

We can create a scatterplot using plt.scatter(x, y), where x and y are the two variables we want to visualize.

x = np.arange(1, 10)
y = np.arange(11, 20)
p = plt.scatter(x, y)

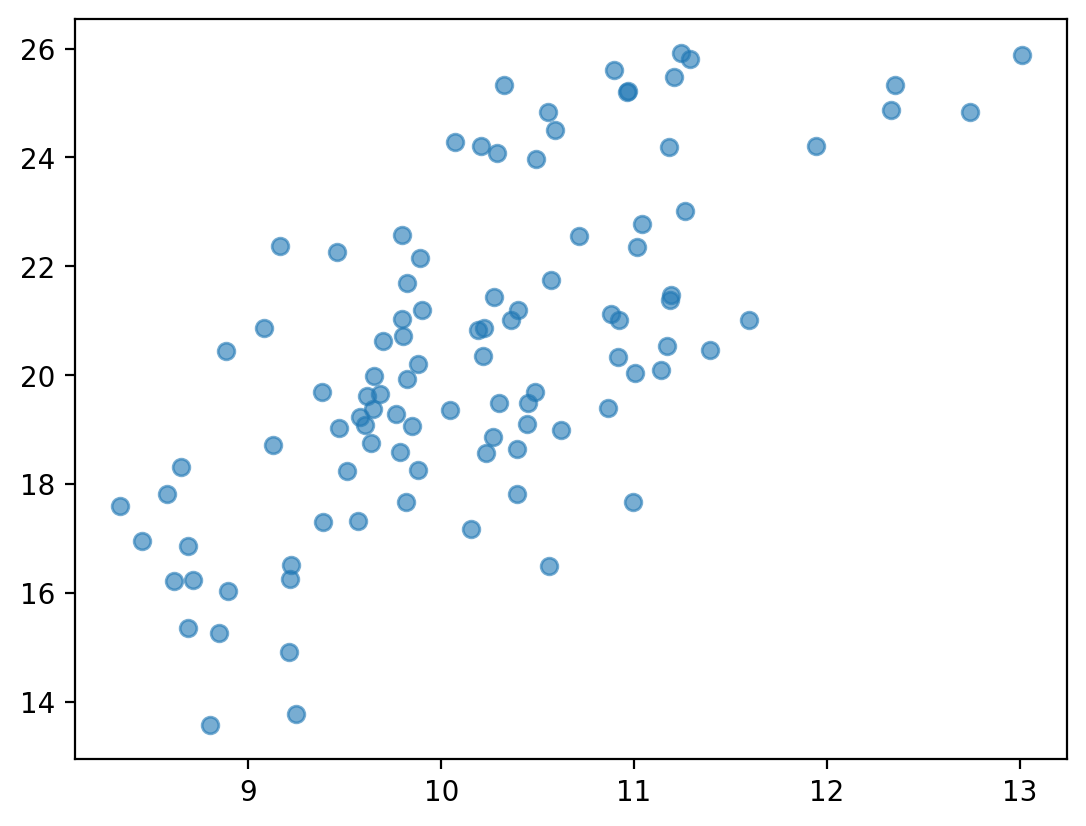
Check-in

Are these variables related? If so, how?

x = np.random.normal(loc = 10, scale = 1, size = 100)
y = x * 2 + np.random.normal(loc = 0, scale = 2, size = 100)
plt.scatter(x, y, alpha = .6)

<matplotlib.collections.PathCollection at 0x1724163d0>

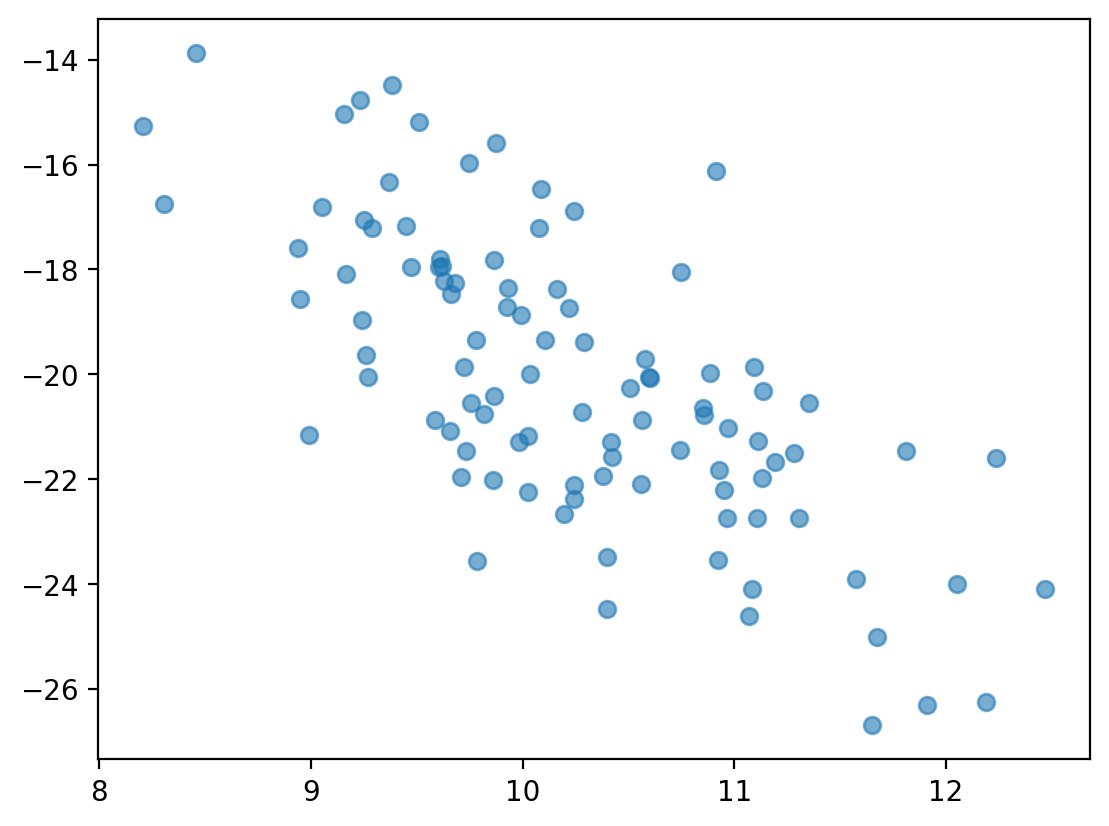
Check-in

Are these variables related? If so, how?

x = np.random.normal(loc = 10, scale = 1, size = 100)
y = -x * 2 + np.random.normal(loc = 0, scale = 2, size = 100)
plt.scatter(x, y, alpha = .6)

<matplotlib.collections.PathCollection at 0x172109d90>

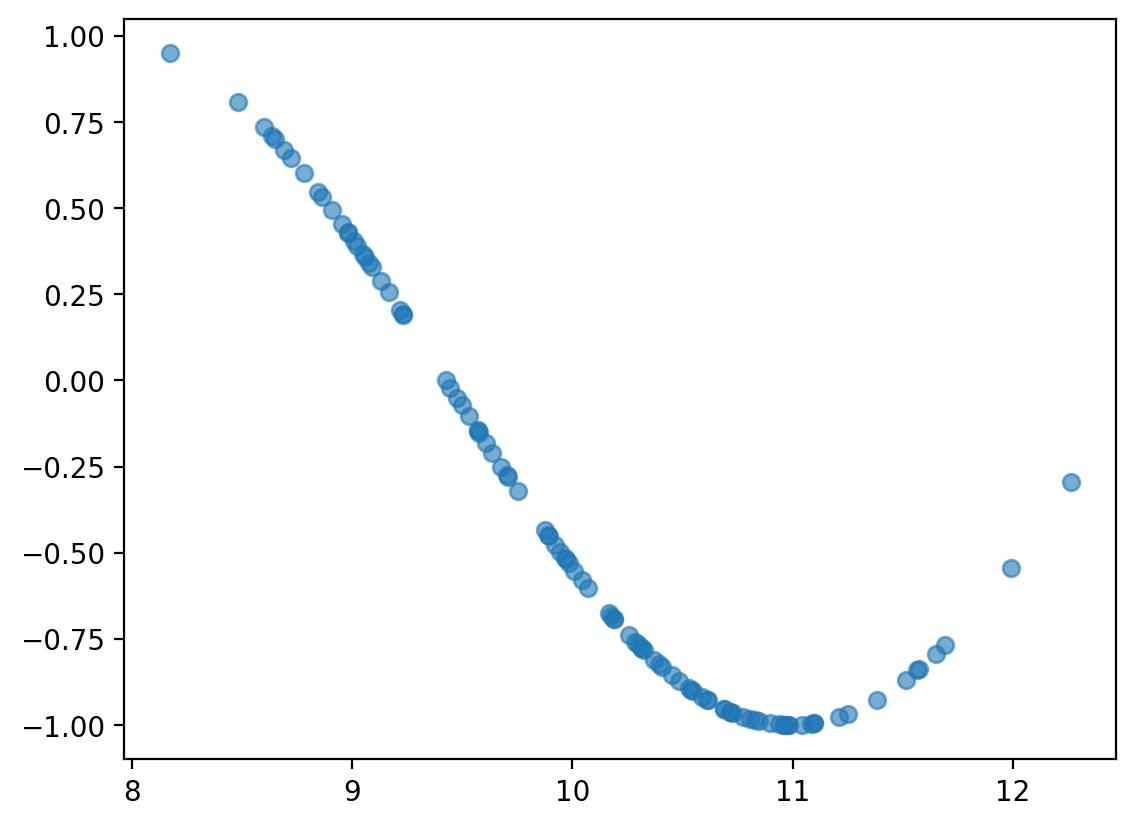
Scatterplots are useful for detecting non-linear relationships

x = np.random.normal(loc = 10, scale = 1, size = 100)
y = np.sin(x)
plt.scatter(x, y, alpha = .6)

<matplotlib.collections.PathCollection at 0x17374df50>

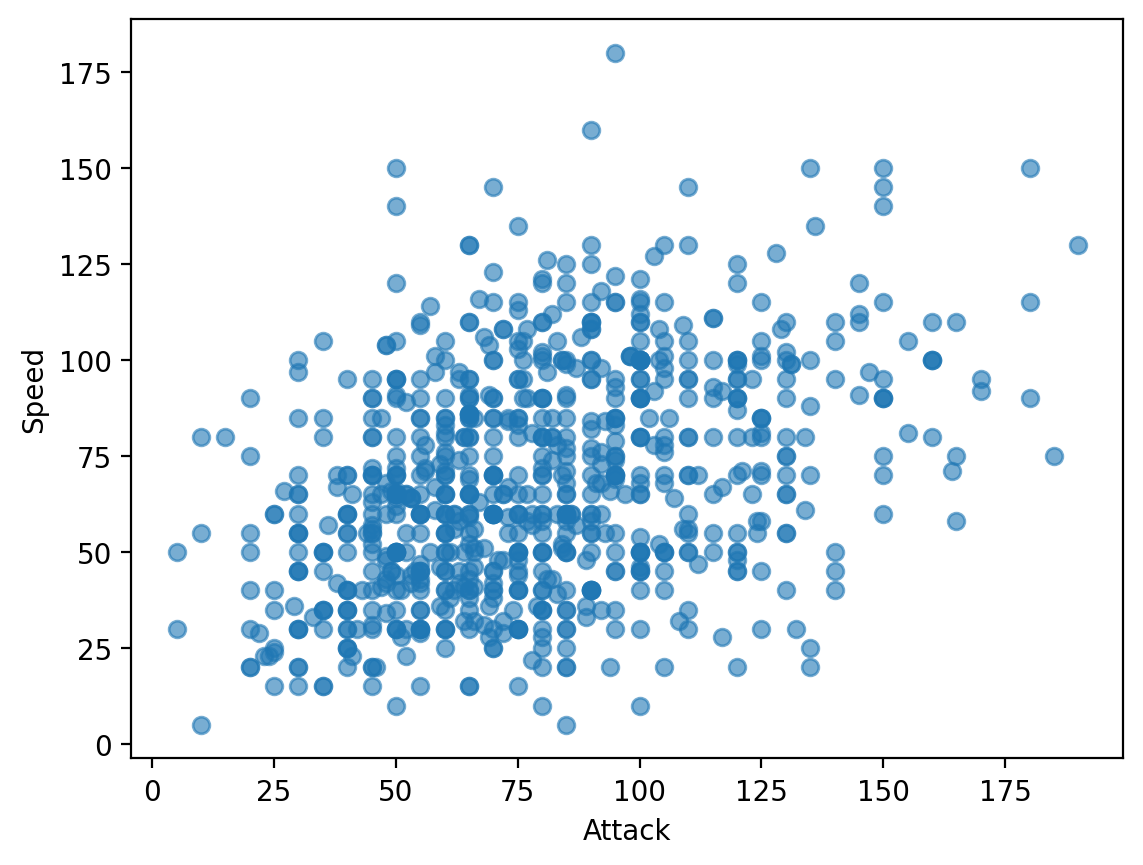
Check-in

How would we visualize the relationship between Attack and Speed in our Pokemon dataset?

### Check-in

Solution

Perhaps somewhat positively correlated, but not too much.

Side note: what would it mean for the Pokemon game if all these attributes (Speed, Defense, etc.) were extremely positively correlated?

plt.scatter(df_pokemon['Attack'], df_pokemon['Speed'], alpha = .6)
plt.xlabel("Attack")
plt.ylabel("Speed")

Text(0, 0.5, 'Speed')

Barplots

What is a barplot?

A barplot visualizes the relationship between one continuous variable and a categorical variable.

• The height of each bar generally indicates the mean of the continuous variable.

• Each bar represents a different level of the categorical variable.

A barplot is a bivariate plot, i.e., it displays at least two variables.

Barplots with matplotlib

plt.bar can be used to create a barplot of our data.

• E.g., average Attack by Legendary status.

• However, we first need to use groupby to calculate the mean Attack per level.

Step 1: Using groupby

summary = df_pokemon[['Legendary', 'Attack']].groupby("Legendary").mean().reset_index()
summary

	Legendary	Attack
0	False	75.669388
1	True	116.676923

### Turn Legendary into a str
summary['Legendary'] = summary['Legendary'].apply(lambda x: str(x))
summary

	Legendary	Attack
0	False	75.669388
1	True	116.676923

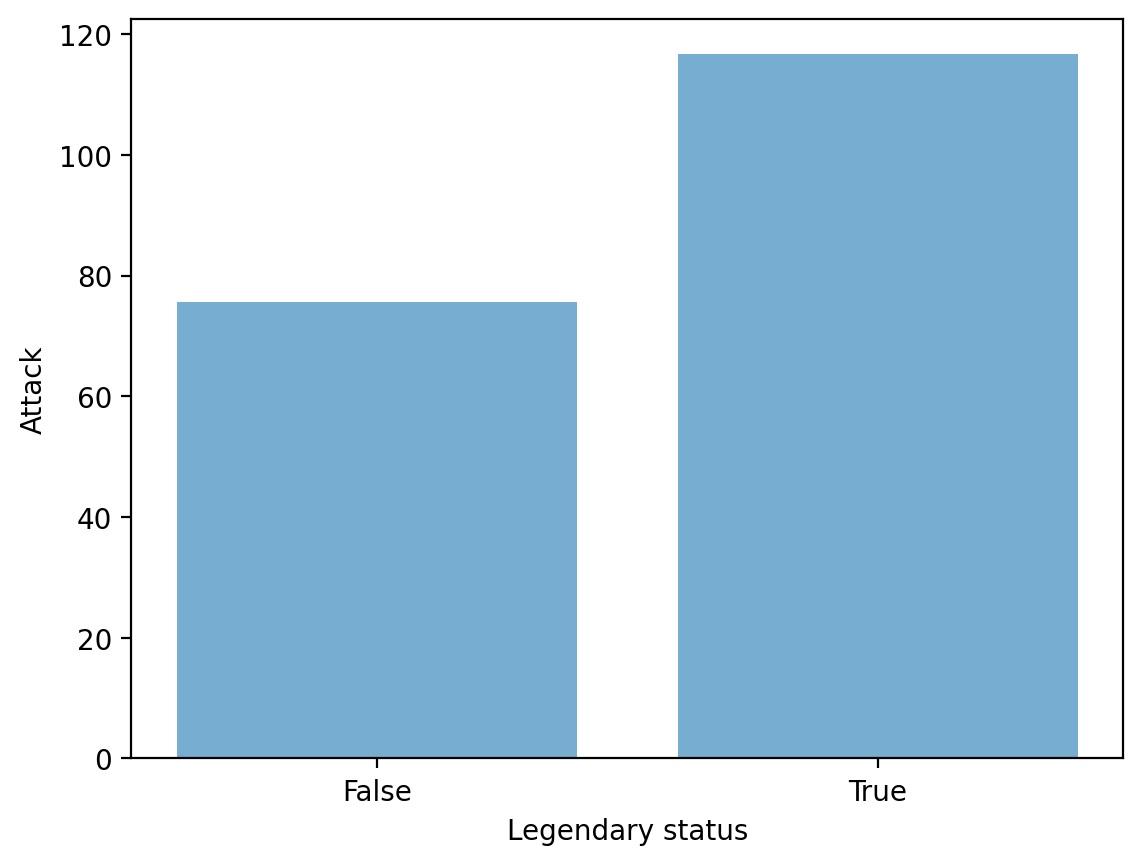
Step 2: Pass values into plt.bar

Check-in:

• What do we learn from this plot?

• What is this plot missing?

plt.bar(x = summary['Legendary'],
       height = summary['Attack'],
       alpha = .6)
plt.xlabel("Legendary status")
plt.ylabel("Attack")

Text(0, 0.5, 'Attack')

Adding error bars

• Without some measure of variance, bar plots just tell us the mean of each level.

• Ideally, we’d have a way to measure how much variance there is around that mean.

Typically, error bars are calculated using the standard error of the mean.

Standard error of the mean

The standard error of the mean is the standard deviation of the distribution of sample means; in practice, it’s an estimate of how much variance there is around our estimate of the mean.

• Standard deviation, or \(\sigma\), is a measure of how much scores deviate around the mean.

• Standard error of the mean, or \(\sigma_\bar{x}\), incorporates standard deviation, but also sample size, or \(n\).

\(\Large \sigma_\bar{x} = \frac{\sigma}{\sqrt{n}}\)

• As \(n\) increases, \(\sigma_\bar{x}\) decreases.

• I.e., larger sample size decreases standard error of the mean––which is good for our estimates!

Turning standard error into error bars

• An error bar represents a “confidence interval”.

• Typically, the lower/upper bounds of a confidence interval are calculated by subtracting or adding \(2 * \sigma_\bar{x}\) to the mean.

Note: Next week, we’ll learn all about why this is!

Step 1: calculate standard errors with sem

sem_summ = df_pokemon[['Legendary', 'Attack']].groupby("Legendary").sem().reset_index()
sem_summ

	Legendary	Attack
0	False	1.124646
1	True	3.764211

### Turn Legendary into a str
sem_summ['Legendary'] = sem_summ['Legendary'].apply(lambda x: str(x))
sem_summ

	Legendary	Attack
0	False	1.124646
1	True	3.764211

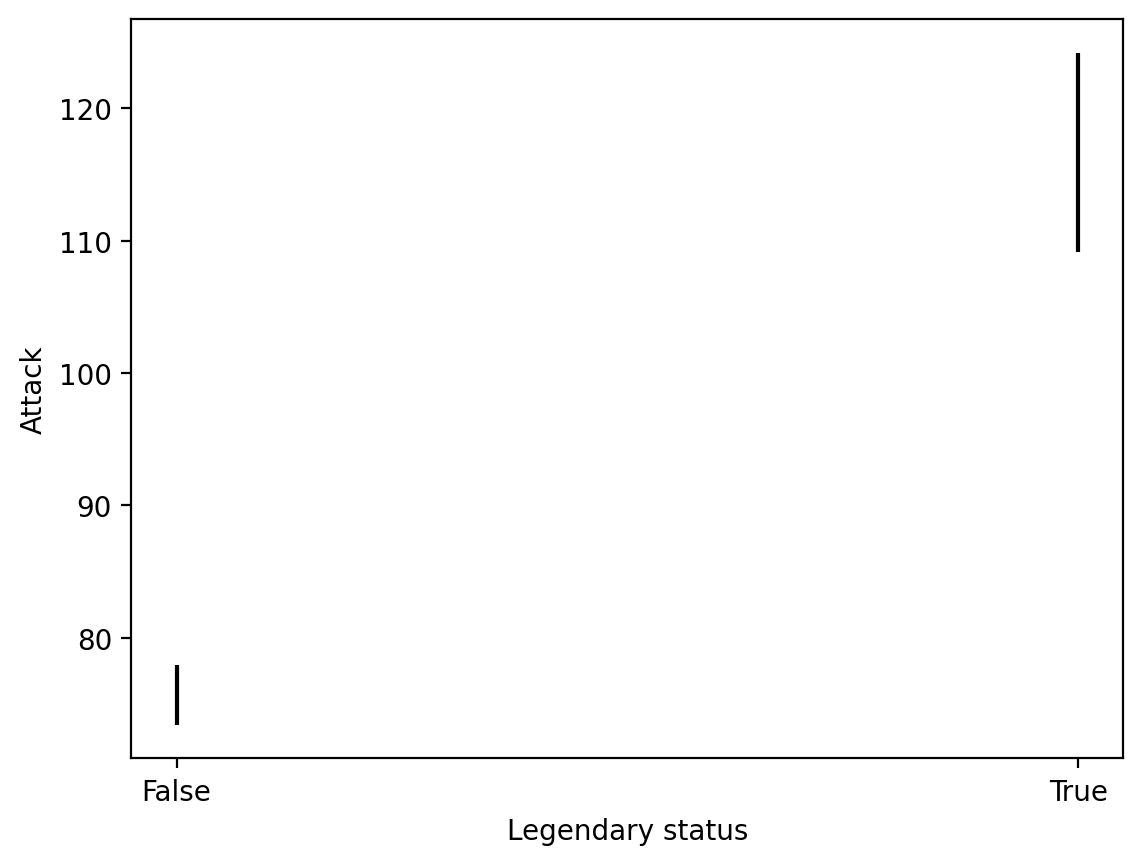
Step 2: Create plot using plt.errorbar

• The x and y coordinates are just from our original summary DataFrame.

• The yerr is the standard error we just calculated.

plt.errorbar(x = summary['Legendary'], # original coordinate
             y = summary['Attack'], # original coordinate
             yerr = sem_summ['Attack'] * 2, # standard error 
            ls = 'none', ## toggle this to connect or not connect the lines
             color = "black"
            )
plt.xlabel("Legendary status")
plt.ylabel("Attack")

Text(0, 0.5, 'Attack')

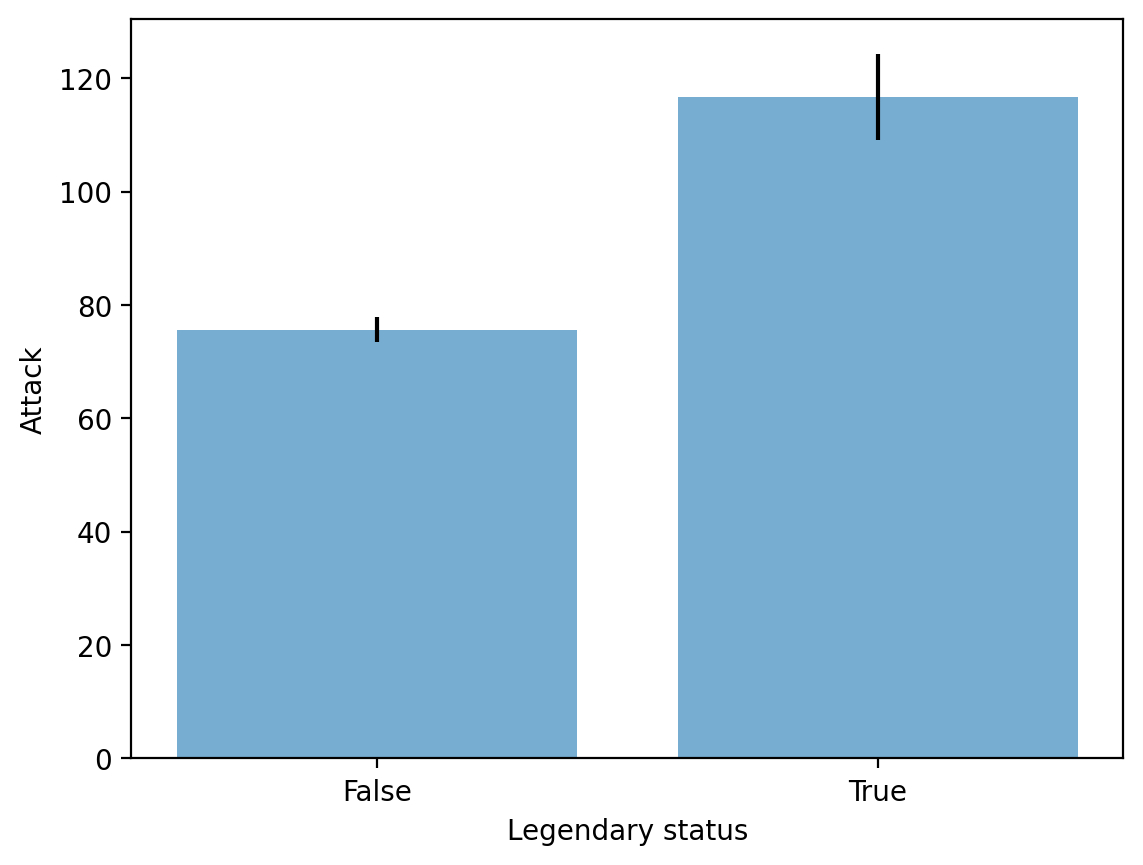
Step 3: Combining with plt.bar

plt.errorbar(x = summary['Legendary'], # original coordinate
             y = summary['Attack'], # original coordinate
             yerr = sem_summ['Attack'] * 2, # standard error 
            ls = 'none', ## toggle this to connect or not connect the lines
             color = "black"
            )
plt.bar(x = summary['Legendary'],
       height = summary['Attack'],
       alpha = .6)
plt.xlabel("Legendary status")
plt.ylabel("Attack")

Text(0, 0.5, 'Attack')

Check-in

Create a barplot with errorbars representing:

• mean Speed by Type 1

• Focusing only on Pokemone with a Type 1 of Grass or Electric.

### Your code here

Solution

This is a multi-step one! Steps involved:

1. Filter our DataFrame to be only Grass or Electric.

2. Use groupby to calculate the mean Speed by Type 1.

3. Use groupby to calculate the standard error of the mean for Speed by Type 1.

4. Use plt.bar and plt.errorbar to plot these data.

Step 1

df_filtered = df_pokemon[df_pokemon['Type 1'].isin(['Grass', 'Electric'])]
df_filtered['Type 1'].value_counts()

Type 1
Grass       70
Electric    44
Name: count, dtype: int64

Steps 2-3

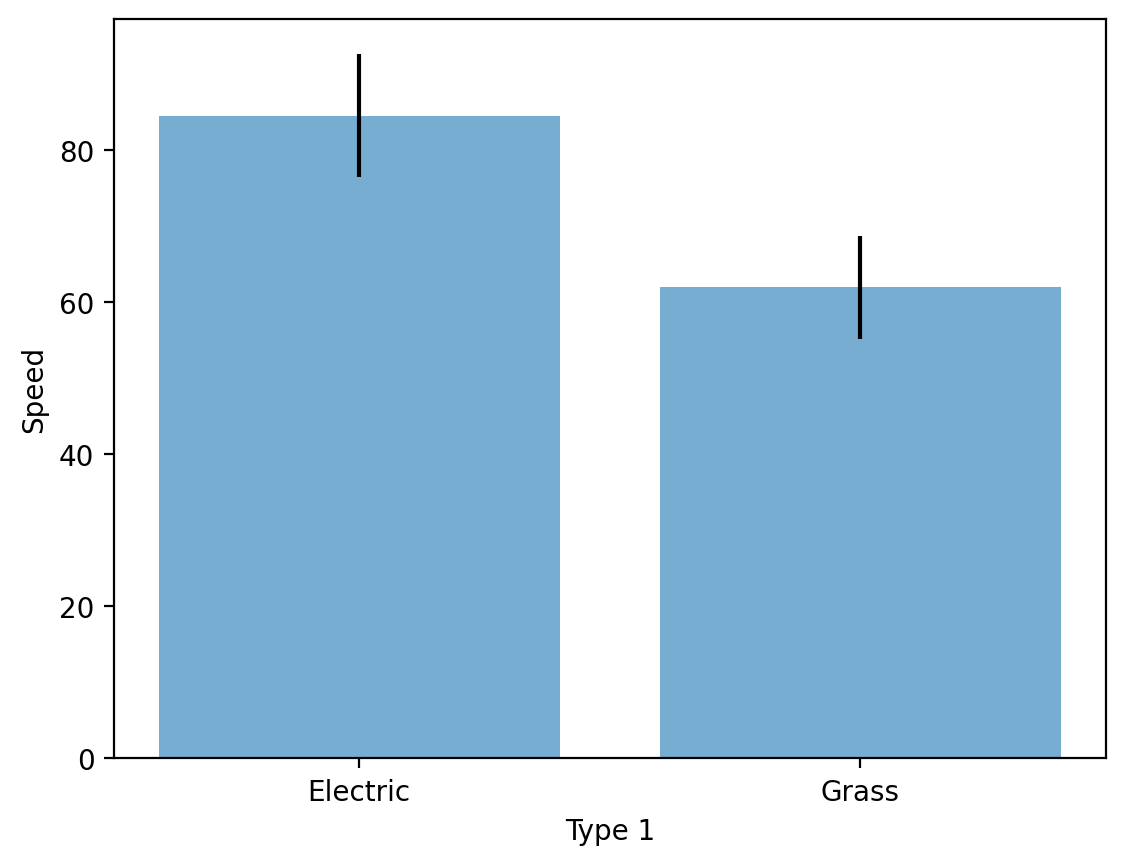
summary = df_filtered[['Type 1', 'Speed']].groupby("Type 1").mean().reset_index()
summary

	Type 1	Speed
0	Electric	84.500000
1	Grass	61.928571

sem_speed = df_filtered[['Type 1', 'Speed']].groupby("Type 1").sem().reset_index()
sem_speed

	Type 1	Speed
0	Electric	4.023911
1	Grass	3.407173

Step 4

plt.errorbar(x = summary['Type 1'], # original coordinate
             y = summary['Speed'], # original coordinate
             yerr = sem_speed['Speed'] * 2, # standard error 
            ls = 'none', color = "black"
            )
plt.bar(x = summary['Type 1'],
       height = summary['Speed'],
       alpha = .6)
plt.xlabel("Type 1")
plt.ylabel("Speed")

Text(0, 0.5, 'Speed')

Conclusion

This concludes our first introduction to data visualization:

• Working with matplotlib.pyplot.

• Creating basic plots: histograms, scatterplots, and barplots.

Next time, we’ll move onto discussing seaborn, another very useful package for data visualization.