Describing Data

Looking back: Exploratory Data Analysis

• In Week 3, we dove deep into data visualization.

• In Week 4, we’ve learned how to wrangle and clean our data.

Now we’ll turn to describing our data––as well as the foundations of statistics.

Goals of this lecture

There are many ways to describe a distribution.

Here, we’ll cover:

• Measures of central tendency: what’s the typical value in this distribution?

• Measures of variability: how much do values differ from each other?

• Detecting (potential) outliers with z-scores.

• Measuring how distributions relate with linear correlations.

Importing relevant libraries

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns ### importing seaborn
import pandas as pd
import scipy.stats as ss

%matplotlib inline 
%config InlineBackend.figure_format = 'retina'

Central Tendency

Central Tendency refers to the “typical value” in a distribution.

Many ways to measure what’s “typical”.

• The mean.

• The median.

• The mode.

Why is this useful?

• A dataset can contain lots of observations.

  • E.g., \(N = 5000\) survey responses about height.

• One way to “describe” this distribution is to visualize it.

• But it’s also helpful to reduce that distribution to a single number.

This is necessarily a simplification of our dataset!

The mean

The arithmetic mean is defined as the sum of all values in a distribution, divided by the number of observations in that distribution.

numbers = [1, 2, 3, 4]
### Calculating the mean by hand
sum(numbers)/len(numbers)

2.5

numpy.mean

The numpy package has a function to calculate the mean on a list or numpy.ndarray.

np.mean(numbers)

2.5

Calculating the mean of a pandas column

If we’re working with a DataFrame, we can calculate the mean of specific columns.

df_gapminder = pd.read_csv("data/viz/gapminder_full.csv")
df_gapminder.head(2)

	country	year	population	continent	life_exp	gdp_cap
0	Afghanistan	1952	8425333	Asia	28.801	779.445314
1	Afghanistan	1957	9240934	Asia	30.332	820.853030

df_gapminder['life_exp'].mean()

59.474439366197174

Check-in

How would you calculate the mean of the gdp_cap column?

### Your code here

Solution

This tells us the average gdp_cap of countries in this dataset across all years measured.

df_gapminder['gdp_cap'].mean()

7215.327081212149

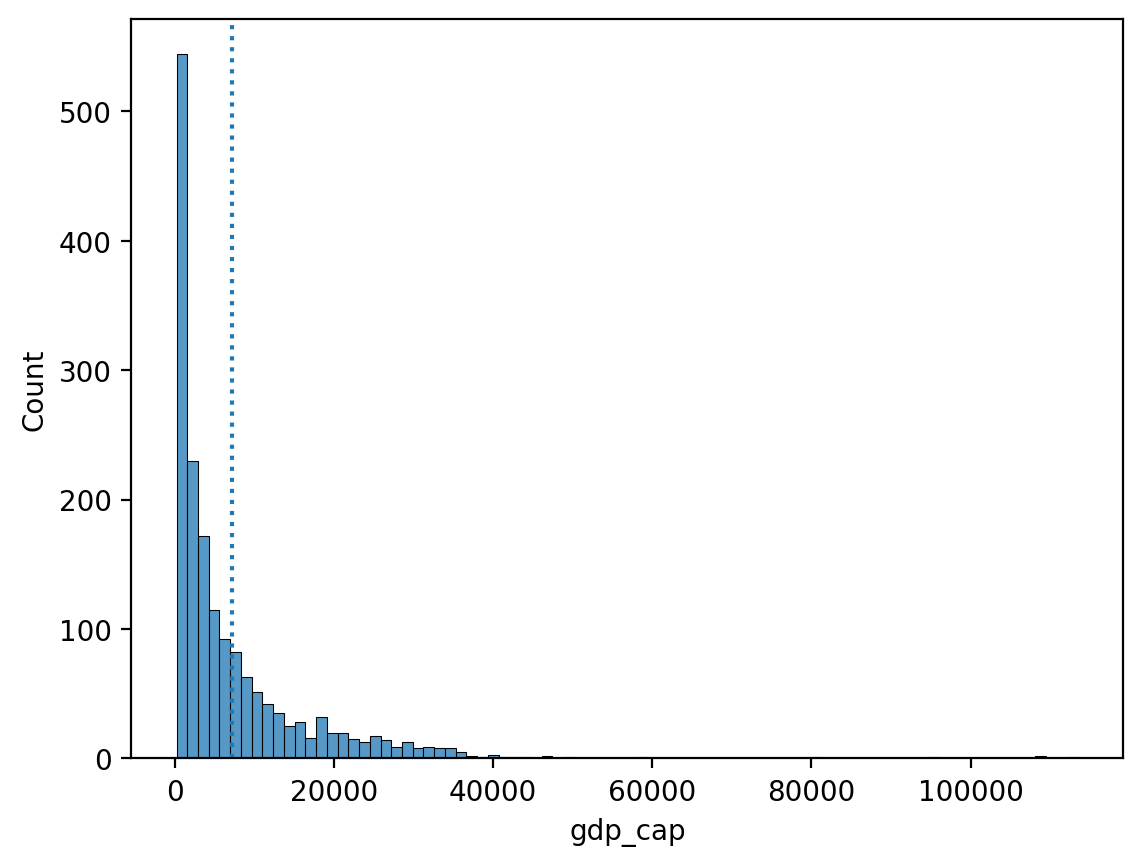
The mean and skew

Skew means there are values elongating one of the “tails” of a distribution.

Of the measures of central tendency, the mean is most affected by the direction of skew.

• How would you describe the skew below?

• Do you think the mean would be higher or lower than the median?

sns.histplot(data = df_gapminder, x = "gdp_cap")
plt.axvline(df_gapminder['gdp_cap'].mean(), linestyle = "dotted")

<matplotlib.lines.Line2D at 0x13ea26d90>

Check-in

Could you calculate the mean of the continent column? Why or why not?

### Your answer here

Solution

• You cannot calculate the mean of continent, which is a categorical variable.

• The mean can only be calculated for continuous variables.

Check-in

• Subtract each observation in numbers from the mean of this list.

• Then, calculate the sum of these deviations from the mean.

What is their sum?

numbers = np.array([1, 2, 3, 4])
### Your code here

Solution

• The sum of deviations from the mean is equal to 0.

• This will be relevant when we discuss standard deviation.

deviations = numbers - numbers.mean()
sum(deviations)

0.0

Interim summary

• The mean is one of the most common measures of central tendency.

• It can only be used for continuous interval/ratio data.

• The sum of deviations from the mean is equal to 0.

• The mean is most affected by skew and outliers.

The median

The median is calculated by sorting all values from least to greatest, then finding the value in the middle.

If there is an even number of values, you take the mean of the middle two values.

df_gapminder['gdp_cap'].median()

3531.8469885

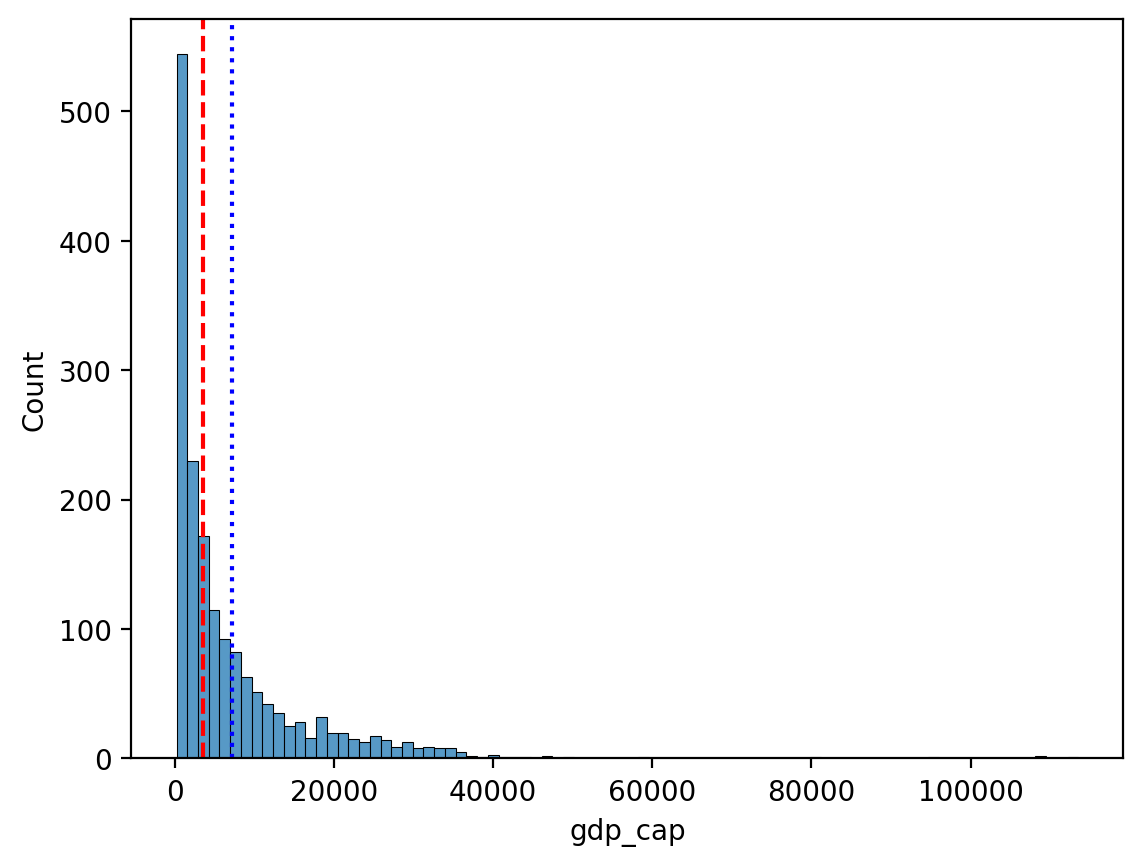
Comparing median and mean

The median is less affected by the direction of skew.

sns.histplot(data = df_gapminder, x = "gdp_cap")
plt.axvline(df_gapminder['gdp_cap'].mean(), linestyle = "dotted", color = "blue")
plt.axvline(df_gapminder['gdp_cap'].median(), linestyle = "dashed", color = "red")

<matplotlib.lines.Line2D at 0x13ebaaa10>

Check-in

Could you calculate the median of the continent column? Why or why not?

### Your answer here

Solution

• You cannot calculate the median of continent, which is a categorical variable.

• The median can only be calculated for ordinal (ranked) or interval/ratio variables.

The mode

The mode is the most frequent value in a dataset.

Unlike the median or mean, the mode can be used with categorical data.

df_pokemon = pd.read_csv("data/pokemon.csv")
### Most common type = Water
df_pokemon['Type 1'].mode()

0    Water
Name: Type 1, dtype: object

mode() returns multiple values?

• If multiple values tie for the most frequent, mode() will return all of them.

• This is because technically, a distribution can have multiple modes!

df_gapminder['gdp_cap'].mode()

0          241.165876
1          277.551859
2          298.846212
3          299.850319
4          312.188423
            ...      
1699     80894.883260
1700     95458.111760
1701    108382.352900
1702    109347.867000
1703    113523.132900
Name: gdp_cap, Length: 1704, dtype: float64

Central tendency: a summary

Measure	Can be used for:	Limitations
Mean	Continuous data	Affected by skew and outliers
Median	Continuous data	Doesn’t include values of all data points in calculation (only ranks)
Mode	Continuous and Categorical data	Only considers the most frequent; ignores other values

Variability

Variability (or dispersion) refers to the degree to which values in a distribution are spread out, i.e., different from each other.

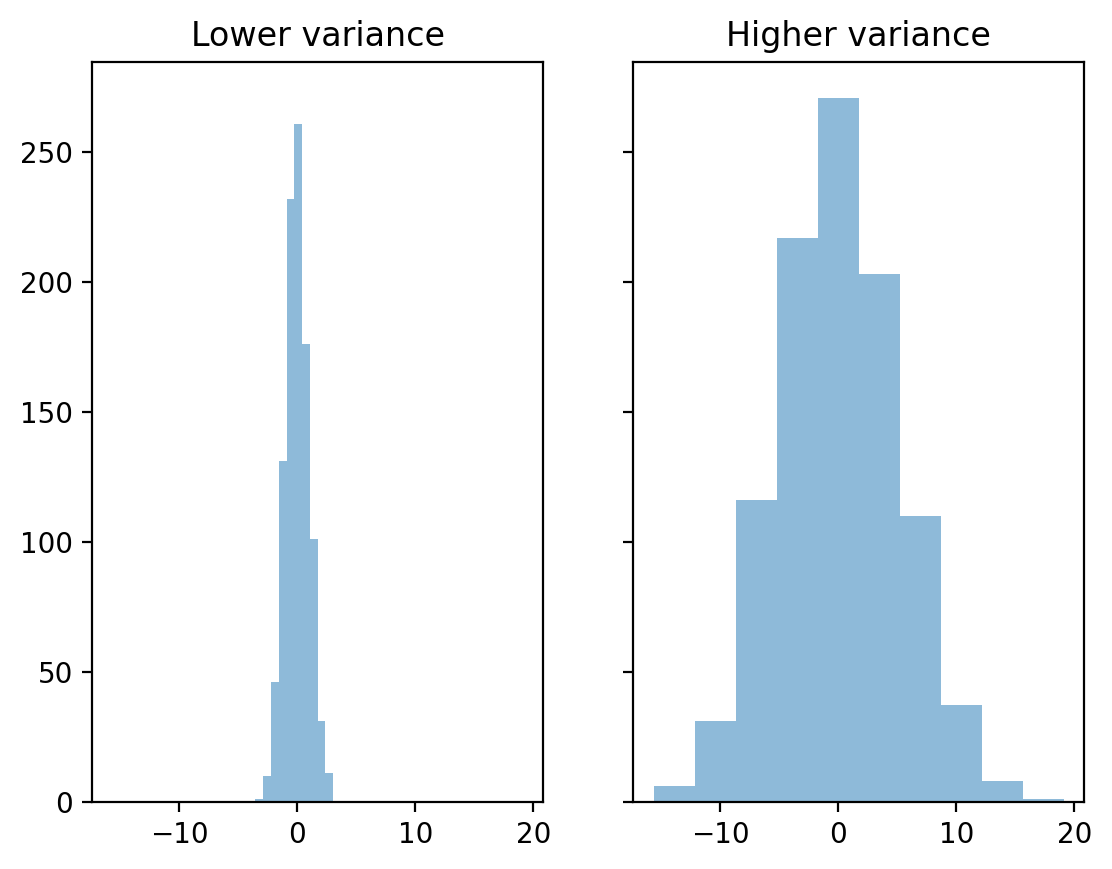
The mean hides variance

Both distributions have the same mean, but different standard deviations.

### Create distributions
d1 = np.random.normal(loc = 0, scale = 1, size = 1000)
d2 = np.random.normal(loc = 0, scale = 5, size = 1000)
### Create subplots
fig, axes = plt.subplots(1, 2, sharex=True, sharey=True)
p1 = axes[0].hist(d1, alpha = .5)
p2 = axes[1].hist(d2, alpha = .5)
axes[0].set_title("Lower variance")
axes[1].set_title("Higher variance")

Text(0.5, 1.0, 'Higher variance')

Capturing variability

There are at least three major approaches to quantifying variability:

• Range: the difference between the maximum and minimum value.

• Interquartile range (IQR): The range of the middle 50% of data.

• Standard deviation: the typical amount that scores deviate from the mean.

Range

Range is the difference between the maximum and minimum value.

Intuitive, but only considers two values in the entire distribution.

d1.max() - d1.min()

6.594707869877328

d2.max() - d2.min()

34.720880205887084

IQR

Interquartile range (IQR) is the difference between the value at the 75% percentile and the value at the 25% percentile.

Focuses on middle 50%, but still only considers two values.

## Get 75% and 25% values
q3, q1 = np.percentile(d1, [75 ,25])
q3 - q1

1.2975812653200791

## Get 75% and 25% values
q3, q1 = np.percentile(d2, [75 ,25])
q3 - q1

6.715031962827277

Standard deviation

Standard deviation (SD) measures the typical amount that scores in a distribution deviate from the mean.

Things to keep in mind:

• SD is the square root of the variance.

• There are actually two measures of SD:

  • Population SD: when you’re measuring the entire population of interest (very rare).

  • Sample SD: when you’re measuring a sample (the typical case); we’ll focus on this one.

Sample SD

The formula for sample standard deviation of \(X\) is as follows:

\(\Large s = \sqrt{\frac{\sum{(X_i - \bar{X})^2}}{n - 1}}\)

• \(n\): number of observations.

• \(\bar{X}\): mean of \(X\).

• \(X_i - \bar{X}\): difference between a particular value of \(X\) and mean.

• \(\sum\): sum of all these squared deviations.

Check-in

The formula involves summing the squared deviations of each value in \(X\) with the mean of \(X\). Why do you think we square these deviations first?

\(\Large\sum{(X_i - \bar{X})^2}\)

### Your answer here

Solution

If you simply summed the raw deviations from the mean, you’d get 0 (this is part of the definition of the mean).

SD, explained

\(\Large s = \sqrt{\frac{\sum{(X_i - \bar{X})^2}}{n - 1}}\)

• First, calculate sum of squared deviations.

  • What is total squared deviation from the mean?

• Then, divide by n - 1: normalize to number of observations.

  • What is average squared deviation from the mean?

• Finally, take the square root:

  • What is average deviation from the mean?

Standard deviation represents the typical or “average” deviation from the mean.

Calculating SD in pandas

df_pokemon['Attack'].std()

32.457365869498425

df_pokemon['HP'].std()

25.534669032332047

Watching out for np.std

• By default, numpy.std will calculate the population standard deviation!

• Must modify the ddof parameter to calculate sample standard deviation.

This is a very common mistake.

### Pop SD
d1.std()

0.9891122146847146

### Sample SD
d1.std(ddof = 1)

0.9896071420185057

Detecting (potential) outliers with z-scores

Defining and detecting outliers is notoriously difficult.

• Sometimes, an observation in a histogram clearly looks like an outlier.

• But how do we quantify this?

What is a z-score?

A z-score is a standardized measure of how many any given point deviates from the mean:

\(Z = \frac{X - \mu}{\sigma}\)

This is useful because it allows us to quantify the standardized distance between some observation and the mean.

Calculating z-scores

## Original distribution
numbers

array([1, 2, 3, 4])

## z-scored distribution
numbers_z = (numbers - numbers.mean()) / numbers.std(ddof=1)
numbers_z

array([-1.161895  , -0.38729833,  0.38729833,  1.161895  ])

Check-in

Can anyone deduce why a z-score would be useful for defining outliers?

Z-scores and outliers

Outliers are data points that differ significantly from other points in a distribution.

• A z-score gives us a standardized measure of how different a given value is from the rest of the distribution.

• We can define thresholds, e.g.:

\(\Large z ≥ |3|\)

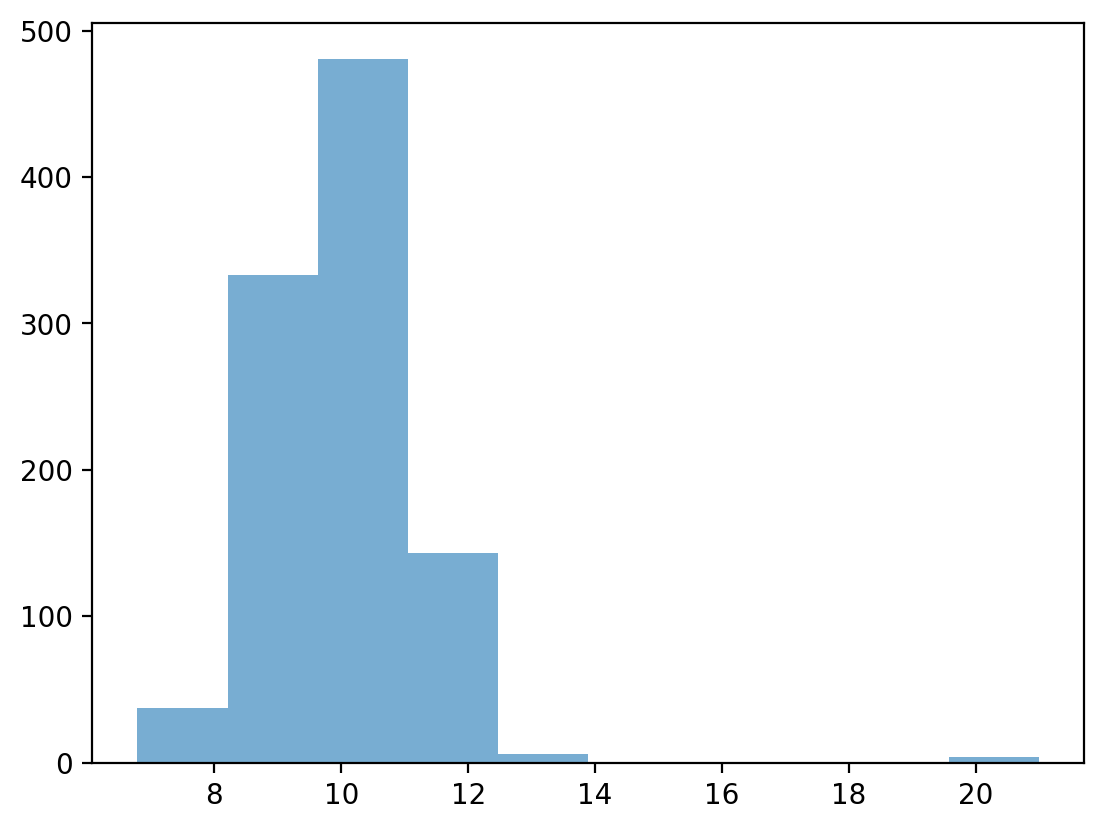
Testing our operationalization

## First, let's define a distribution with some possible outliers
norm = np.random.normal(loc = 10, scale = 1, size = 1000)
upper_outliers = np.array([21, 21, 21, 21]) ## some random outliers
data = np.concatenate((norm, upper_outliers))
p = plt.hist(data, alpha = .6)

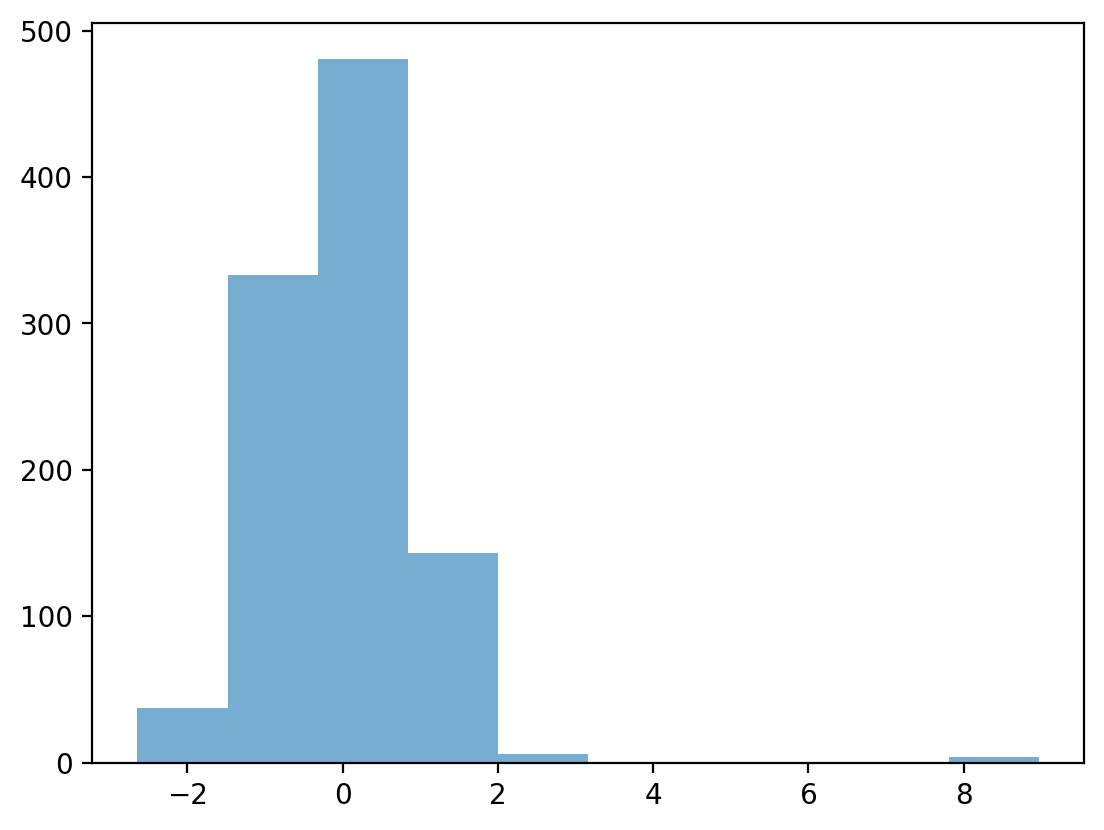
Z-scoring our distribution

What is the z-score of the values way off to the right?

data_z = (data - data.mean()) / data.std(ddof=1)
p = plt.hist(data_z, alpha = .6)

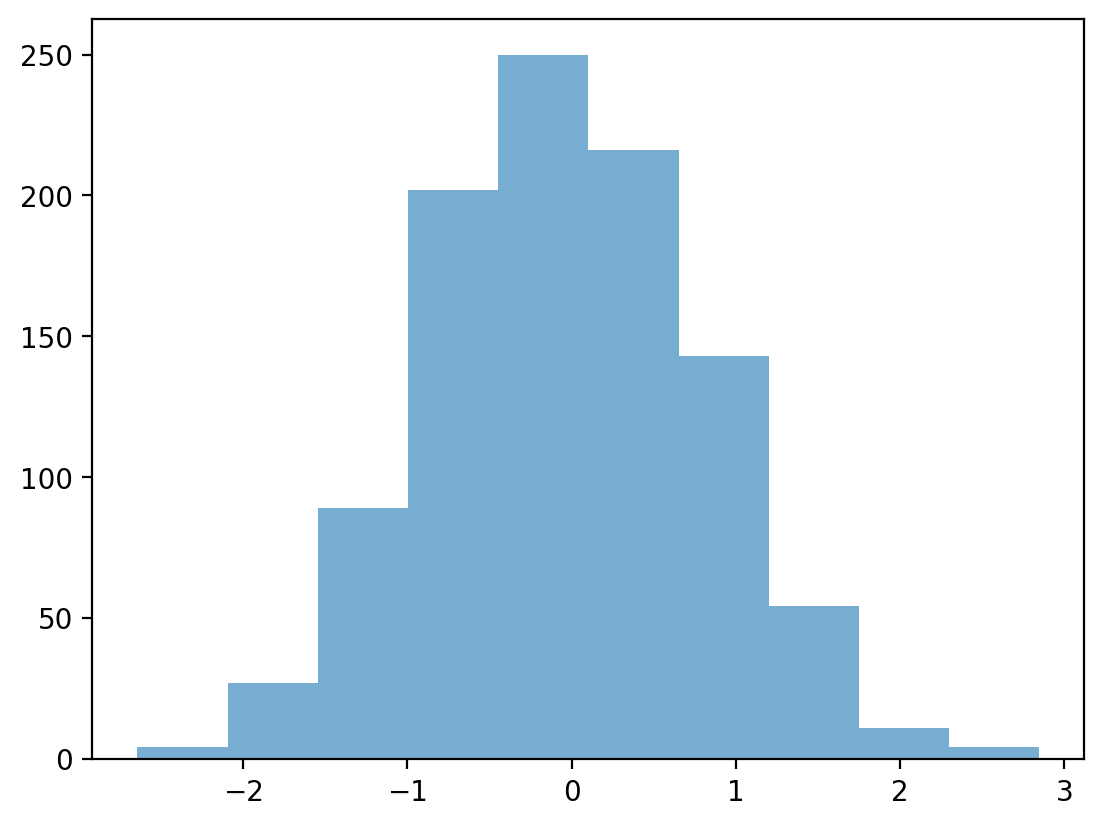
Removing outliers

data_z_filtered = data_z[abs(data_z)<=3]
p = plt.hist(data_z_filtered, alpha = .6)

Check-in

Can anyone think of challenges or problems with this approach to detecting outliers?

Caveats, complexity, and context

• There is not a single unifying definition of what an outlier is.

• Depending on the shape of the distribution, removing observations where \(z > |3|\) might be removing important data.

  • E.g., in a skewed distribution, we might just be “cutting off the tail”.

• Even if the values do seem like outliers, there’s a philosophical question of why and what that means.

  • Are those values “random”? What’s the underlying *data-generating process?

This is why statistics is not a mere matter of applying formulas. Context always matters!

Describing bivariate data with correlations

• So far, we’ve been focusing on univariate data: a single distribution.

• What if we want to describe how two distributions relate to each other?

  • For today, we’ll focus on continuous distributions.

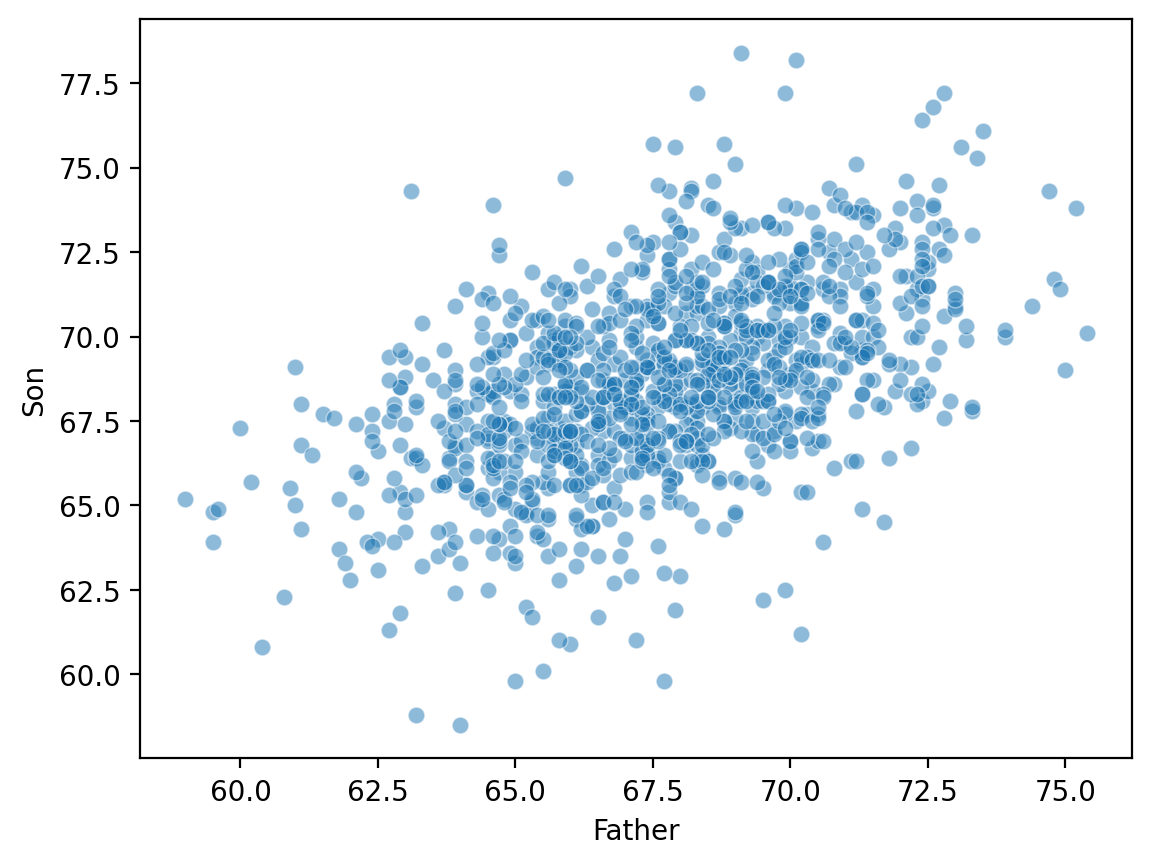
Bivariate relationships: height

• A classic example of continuous bivariate data is the height of a parent and child.

• These data were famously collected by Karl Pearson.

df_height = pd.read_csv("data/wrangling/height.csv")
df_height.head(2)

	Father	Son
0	65.0	59.8
1	63.3	63.2

Plotting Pearson’s height data

sns.scatterplot(data = df_height, x = "Father", y = "Son", alpha = .5)

<Axes: xlabel='Father', ylabel='Son'>

Introducing linear correlations

A correlation coefficient is a number between \([–1, 1]\) that describes the relationship between a pair of variables.

Specifically, Pearson’s correlation coefficient (or Pearson’s \(r\)) describes a (presumed) linear relationship.

Two key properties:

• Sign: whether a relationship is positive (+) or negative (–).

• Magnitude: the strength of the linear relationship.

Calculating Pearson’s \(r\) with scipy

scipy.stats has a function called pearsonr, which will calculate this relationship for you.

Returns two numbers:

• \(r\): the correlation coefficent.

• \(p\): the p-value of this correlation coefficient, i.e., whether it’s significantly different from 0.

ss.pearsonr(df_height['Father'], df_height['Son'])

PearsonRResult(statistic=0.5011626808075925, pvalue=1.2729275743650796e-69)

Check-in

Using scipy.stats.pearsonr (here, ss.pearsonr), calculate Pearson’s \(r\) for the relationship between the Attack and Defense of Pokemon.

• Is this relationship positive or negative?

• How strong is this relationship?

### Your code here

Solution

ss.pearsonr(df_pokemon['Attack'], df_pokemon['Defense'])

PearsonRResult(statistic=0.43868705511848904, pvalue=5.8584798642904e-39)

Check-in

Pearson’r \(r\) measures the linear correlation between two variables. Can anyone think of potential limitations to this approach?

Limitations of Pearson’s \(r\)

• Pearson’s \(r\) presumes a linear relationship and tries to quantify its strength and direction.

• But many relationships are non-linear!

• Unless we visualize our data, relying only on Pearson’r \(r\) could mislead us.

Non-linear data where \(r = 0\)

x = np.arange(1, 40)
y = np.sin(x)
p = sns.lineplot(x = x, y = y)

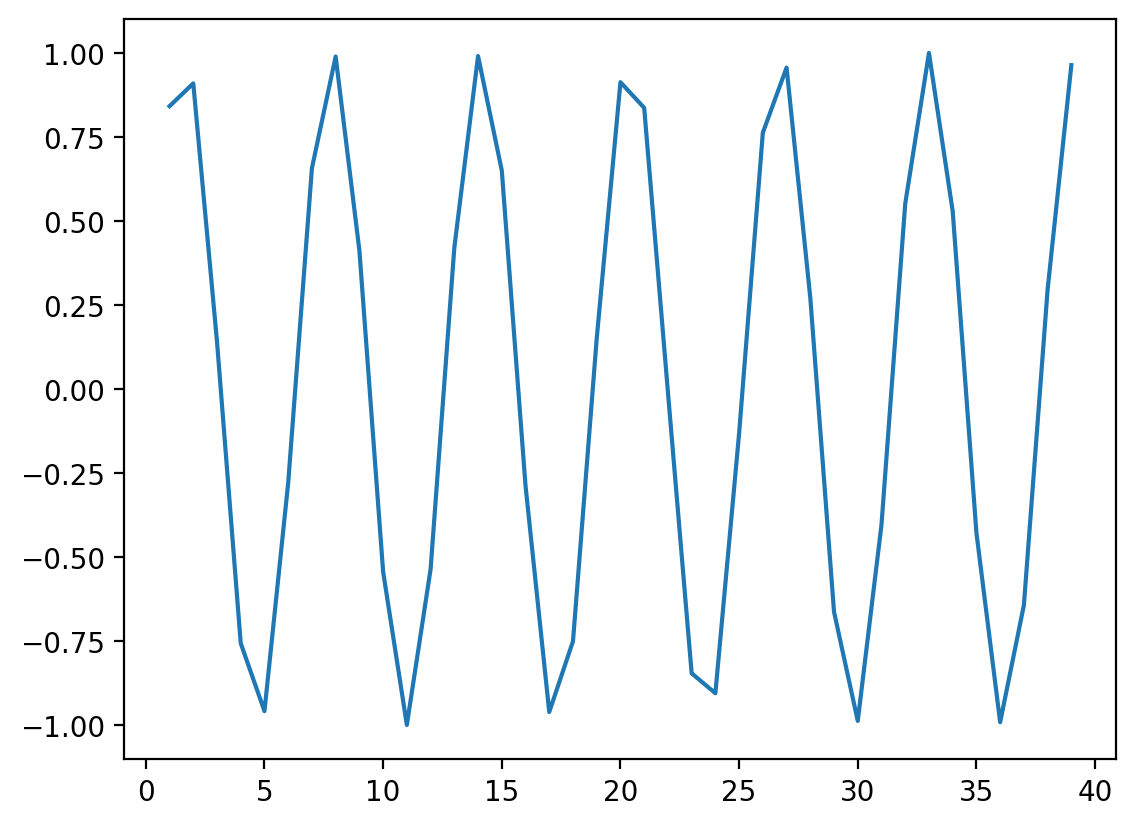
### r is close to 0, despite there being a clear relationship!
ss.pearsonr(x, y)

PearsonRResult(statistic=-0.04067793461845846, pvalue=0.8057827185936635)

When \(r\) is invariant to the real relationship

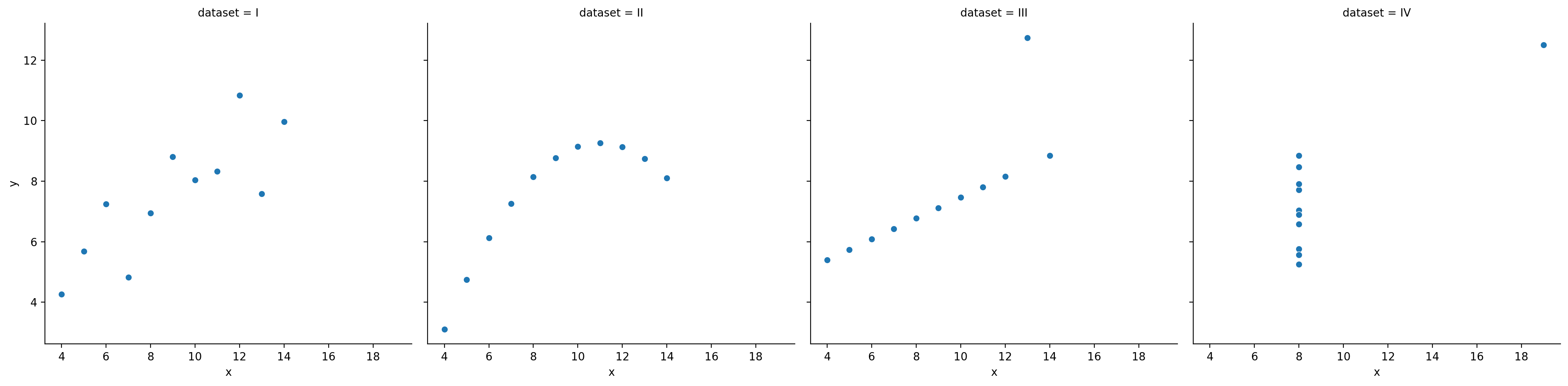
All these datasets have roughly the same correlation coefficient.

df_anscombe = sns.load_dataset("anscombe")
sns.relplot(data = df_anscombe, x = "x", y = "y", col = "dataset")

/Users/seantrott/anaconda3/lib/python3.11/site-packages/seaborn/axisgrid.py:118: UserWarning: The figure layout has changed to tight
  self._figure.tight_layout(*args, **kwargs)

<seaborn.axisgrid.FacetGrid at 0x13ee950d0>

Conclusion

There are many ways to describe our data:

• Measuring its central tendency.

• Measuring its variability.

• Measuring how it correlates with other data.

All of these are useful, and all are also simplifications.